卷 2
填空题
1~6小题,每小题4分,共24分
1
设
y=(1+sinx)x
,则
dyx=π=
______.
【答案】
−πdx
【解析】
两边取对数得
lny=xln(1+sinx)
。对
x
求导得
y1⋅y′=ln(1+sinx)+1+sinxxcosx,
于是导函数
y′=(1+sinx)x⋅[ln(1+sinx)+x⋅1+sinxcosx].
故
dy∣x=π=y′(π)dx=−πdx
。
2
曲线
y=x(1+x)3/2
的斜渐近线方程为 ______.
【答案】
y=x+23
【解析】
为了求曲线
y=x(1+x)3/2
的斜渐近线,考虑
x→∞
时的行为。斜渐近线的一般形式为
y=mx+b
,其中
m=limx→∞xy
,
b=limx→∞(y−mx)
。
首先,计算
m
:
m=x→∞limxy=x→∞limxx(1+x)3/2=x→∞limx3/2(1+x)3/2=x→∞lim(x1+x)3/2=x→∞lim(1+x1)3/2=1 然后,计算
b
:
b=x→∞lim(y−mx)=x→∞lim(x(1+x)3/2−x) 将
y
改写为
y=x(1+x1)3/2
,则
b=x→∞limx((1+x1)3/2−1)
令
u=x1
,当
x→∞
时
u→0+
,则
b=u→0limu(1+u)3/2−1
该极限是函数
f(u)=(1+u)3/2
在
u=0
处的导数,即
f′(u)=23(1+u)1/2,f′(0)=23
因此,
b=23
。
故斜渐近线方程为
y=x+23
。
3
【答案】
4π
【解析】
令
x=sinθ
,则
dx=cosθdθ
,且当
x=0
时
θ=0
,当
x=1
时
θ=2π
。代入积分得:
∫01(2−x2)1−x2xdx=∫0π/2(2−sin2θ)⋅cosθsinθ⋅cosθdθ=∫0π/22−sin2θsinθdθ. 再令
u=cosθ
,则
du=−sinθdθ
,即
sinθdθ=−du
,且当
θ=0
时
u=1
,当
θ=2π
时
u=0
。代入得:
∫0π/22−sin2θsinθdθ=∫102−(1−u2)−du=∫101+u2−du=∫011+u2du.
计算该积分:
∫011+u2du=arctanu01=arctan1−arctan0=4π−0=4π. 因此,原积分的值为
4π
。
4
同试卷 1 第 2 题
5
当
x→0
时,
α(x)=kx2
与
β(x)=1+xarcsinx−cosx
是等价无穷小,
则
k=
______.
【答案】
43
【解析】
由于
α(x)=kx2
与
β(x)=1+xarcsinx−cosx
是等价无穷小,当
x→0
时,有:
x→0limα(x)β(x)=1
即:
x→0limkx21+xarcsinx−cosx=1 令:
L=x→0limx21+xarcsinx−cosx 则
k=L
。为计算
L
,对分子有理化:
1+xarcsinx−cosx=1+xarcsinx+cosx(1+xarcsinx)−cosx 代入极限:
L=x→0limx2(1+xarcsinx+cosx)1+xarcsinx−cosx 当
x→0
时,分母中
1+xarcsinx+cosx→2
,因此:
L=21x→0limx21+xarcsinx−cosx
令:
M=x→0limx21+xarcsinx−cosx
使用泰勒展开计算
M
。当
x→0
时:
arcsinx=x+6x3+O(x5),cosx=1−2x2+24x4+O(x6)
于是:
xarcsinx=x2+6x4+O(x6)
代入分子:
1+xarcsinx−cosx=1+(x2+6x4)−(1−2x2+24x4)+O(x6)=23x2+81x4+O(x6)
因此:
x21+xarcsinx−cosx=23+81x2+O(x4)→23(x→0)
所以
M=23
,代入得:
L=21×23=43
故
k=43
。
验证:使用洛必达法则计算
M
,结果同样为
23
,确认无误。
6
同试卷 1 第 5 题
选择题
7~14小题,每小题4分,共32分
7
同试卷 1 第 7 题
8
同试卷 1 第 8 题
9
设函数
y=y(x)
由参数方程
{x=t2+2t,y=ln(1+t)
确定,则曲线
y=y(x)
在
x=3
处的法线与
x
轴交点的横坐标是
正确答案:A【解析】 首先,由参数方程
x=t2+2t
和
y=ln(1+t)
确定曲线。当
x=3
时,解方程
t2+2t=3
,得
t2+2t−3=0
,解得
t=1
或
t=−3
。但
t=−3
时
y=ln(1−3)=ln(−2)
无意义,故取
t=1
,对应点
(3,ln2)
。
求导数
dxdy
:
dtdy=1+t1
,
dtdx=2t+2
,
所以
dxdy=dx/dtdy/dt=2t+21/(1+t)=2(1+t)21
。
在
t=1
时,
dxdy=2(1+1)21=81
,即切线斜率为
81
,故法线斜率为
−8
。
法线方程为
y−ln2=−8(x−3)
。
求与
x
轴交点,令
y=0
:
0−ln2=−8(x−3)
,
即
−ln2=−8(x−3)
,
解得
x−3=8ln2
,
所以
x=3+81ln2
,
对应选项 A。
10
设区域
D={(x,y)x2+y2≤4,x≥0,y≥0}
,
f(x)
为
D
上的正值连续函数,
a,b
为常数,则
∬Df(x)+f(y)af(x)+bf(y)dσ=
正确答案:D【解析】
考虑积分
I=∬Df(x)+f(y)af(x)+bf(y)dσ
。由于区域
D={(x,y)∣x2+y2≤4,x≥0,y≥0}
关于直线
y=x
对称,且
f
为正值连续函数,交换
x
和
y
得
J=∬Df(x)+f(y)bf(x)+af(y)dσ=I. 计算
I+J
:
I+J=∬Df(x)+f(y)af(x)+bf(y)+bf(x)+af(y)dσ=∬Df(x)+f(y)(a+b)(f(x)+f(y))dσ=∬D(a+b)dσ. 区域
D
是半径为 2 的四分之一圆,面积为
π
,故
I+J=(a+b)π.
由于
I=J
,有
2I=(a+b)π
,所以
I=2a+bπ.
因此,正确答案为 D。
11
同试卷 1 第 9 题
12
设函数
f(x)=ex−1x−11
,则
正确答案:D【解析】
函数
f(x)=ex−1x−11
在
x=0
和
x=1
处无定义,因此这两点为间断点。
对于
x=1
,计算左右极限:
- 当
x→1+
时,
x−1x→+∞
,
ex−1x→+∞
,故
f(x)→0
;
- 当
x→1−
时,
x−1x→−∞
,
ex−1x→0
,故
f(x)→−1
。
左右极限均存在但不相等,因此
x=1
为第一类间断点。
对于
x=0
,计算左右极限:
- 当
x→0+
时,
x−1x→0−
,
ex−1x→1−
,故
f(x)→−∞
;
- 当
x→0−
时,
x−1x→0+
,
ex−1x→1+
,故
f(x)→+∞
。
左右极限均不存在(趋于无穷),因此
x=0
为第二类间断点。
综上,选项 D 正确。
13
同试卷 1 第 11 题
14
同试卷 1 第 12 题
解答题
15~23小题,共94分
15
(本题满分 11 分)
设函数
f(x)
连续,且
f(0)=0
,
求极限
x→0limx∫0xf(x−t)dt∫0x(x−t)f(t)dt
【答案】
21
【解析】
给定极限
limx→0x∫0xf(x−t)dt∫0x(x−t)f(t)dt
,其中
f(x)
连续且
f(0)=0
。
首先,简化分母中的积分:令
u=x−t
,则当
t=0
时
u=x
,当
t=x
时
u=0
,且
dt=−du
,因此
∫0xf(x−t)dt=∫x0f(u)(−du)=∫0xf(u)du.
所以分母变为
x∫0xf(u)du
.
分子为
∫0x(x−t)f(t)dt
,可写为
∫0x(x−t)f(t)dt=x∫0xf(t)dt−∫0xtf(t)dt.
因此极限化为
x→0limx∫0xf(t)dtx∫0xf(t)dt−∫0xtf(t)dt=x→0lim(1−x∫0xf(t)dt∫0xtf(t)dt).
令
L=limx→0x∫0xf(t)dt∫0xtf(t)dt
,该极限为
00
型,应用洛必达法则。令
F(x)=∫0xtf(t)dt
,则
F′(x)=xf(x)
;令
G(x)=x∫0xf(t)dt
,则
G′(x)=∫0xf(t)dt+xf(x)
。于是
L=x→0limG′(x)F′(x)=x→0lim∫0xf(t)dt+xf(x)xf(x).
由于
f
连续且
f(0)=0
,有
∫0xf(t)dt=f(0)x+o(x)
和
xf(x)=f(0)x+o(x)
,代入得
L=x→0lim2f(0)x+o(x)f(0)x+o(x)=2f(0)f(0)=21.
因此原极限为
1−L=1−21=21.
16
(本题满分 11 分)
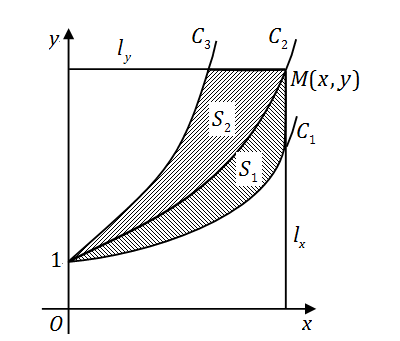
如图,
C1
和
C2
分别是
y=21(1+ex)
和
y=ex
的图象,
过点(0,1)的曲线
C3
是一单调增函数的图象.
过
C2
上任一点
M(x,y)
分别作垂直于
x
轴和
y
轴的直线
lx
和
ly
.
记
C1
,
C2
与
lx
所围图形的面积为
S1(x)
;
C2
,
C3
与
ly
所围图形的面积为
S2(y)
.
如果总有
S1(x)=S2(y)
,求曲线
C3
的方程
x=ϕ(y)
.
【答案】
x=lny+21−2y1
【解析】
由题意,曲线
C1
的方程为
y=21(1+ex)
,曲线
C2
的方程为
y=ex
。过点
M(x,y)
在
C2
上作垂直于
x
轴的直线
lx
和垂直于
y
轴的直线
ly
。
面积
S1(x)
是
C1
、
C2
与
lx
所围图形的面积,即从
x=0
到
x
的
C2
与
C1
之间的区域面积:
S1(x)=∫0x[et−21(1+et)]dt=∫0x21(et−1)dt=21[et−t]0x=21(ex−x−1)
面积
S2(y)
是
C2
、
C3
与
ly
所围图形的面积,即从
y=1
到
y
的
C3
与
C2
之间的区域面积。设
C3
的方程为
x=ϕ(y)
,则:
S2(y)=∫1y[ϕ(u)−lnu]du
由条件
S1(x)=S2(y)
且
y=ex
,代入得:
21(ex−x−1)=∫1ex[ϕ(u)−lnu]du
令
t=ex
,则
x=lnt
,对于
t>1
:
21(t−lnt−1)=∫1t[ϕ(u)−lnu]du
两边对
t
求导:
dtd[21(t−lnt−1)]=21(1−t1)
dtd∫1t[ϕ(u)−lnu]du=ϕ(t)−lnt
所以:
ϕ(t)−lnt=21(1−t1)
解得:
ϕ(t)=lnt+21−2t1
因此,曲线
C3
的方程为
x=ϕ(y)=lny+21−2y1
。
验证:当
y=1
时,
x=ln1+21−21=0
,过点
(0,1)
,且
ϕ′(y)=y1+2y21>0
,为单调增函数,符合题意。
17
(本题满分 11 分)
同试卷 1 第 17 题
18
(本题满分 12 分)
用变量代换
x=cost
(
0<t<π
)化简微分方程
(1−x2)y′′−xy′+y=0
,
并求其满足
yx=0=1
,
y′x=0=2
的特解.
【答案】
y(x)=2x+1−x2
【解析】
给定微分方程
(1−x2)y′′−xy′+y=0
,使用变量代换
x=cost
(其中
0<t<π
)。
首先,计算
y′
和
y′′
关于
t
的表达式。
由
x=cost
,得
dtdx=−sint
。
于是,
y′=dxdy=dtdy⋅dxdt=−sint1dtdy
令
y˙=dtdy
,则
y′=−sint1y˙
。
进一步求
y′′
:
y′′=dxd(y′)=dtd(−sint1y˙)⋅dxdt=(sin2tcosty˙−sint1y¨)⋅(−sint1)=sin2t1y¨−sin3tcosty˙
其中
y¨=dt2d2y
。
代入原方程:
(1−x2)y′′−xy′+y=sin2t⋅(sin2t1y¨−sin3tcosty˙)−cost⋅(−sint1y˙)+y=y¨−sintcosty˙+sintcosty˙+y=y¨+y=0
因此,化简后的微分方程为
y¨+y=0
。
该方程的通解为
y(t)=Acost+Bsint
,其中
A
和
B
为常数。
由初始条件
y∣x=0=1
和
y′∣x=0=2
,且
x=cost
,当
x=0
时
t=2π
。
在
t=2π
处:
y(t)=Acos2π+Bsin2π=B=1
所以
B=1
。
接下来,求
y′
关于
x
的表达式:
y′=−sint1y˙=−sint1(−Asint+Bcost)=A−Bcott
在
t=2π
处,
cot2π=0
,故
y′∣x=0=A=2
所以
A=2
。
因此,特解为
y(t)=2cost+sint
。
代回
x=cost
,且
sint=1−cos2t=1−x2
(因为
0<t<π
,
sint>0
),得
这就是满足初始条件的特解。
19
(本题满分 12 分)
同试卷 1 第 18 题
20
(本题满分 10 分)
已知函数
z=f(x,y)
的全微分
dz=2xdx−2ydy
,并且
f(1,1)=2
.
求
f(x,y)
在椭圆域
D={(x,y)x2+4y2≤1}
上的最大值和最小值.
【答案】
最大值:3,最小值:-2
【解析】
由全微分
dz=2xdx−2ydy
可得偏导数
∂x∂f=2x
,
∂y∂f=−2y
。积分得
f(x,y)=x2+g(y)
,代入偏导数有
g′(y)=−2y
,积分得
g(y)=−y2+C
,故
f(x,y)=x2−y2+C
。利用条件
f(1,1)=2
得
C=2
,因此
f(x,y)=x2−y2+2
。
在椭圆域
D={(x,y)x2+4y2≤1}
上求最值。先求内部驻点:令
fx=2x=0
,
fy=−2y=0
,得驻点
(0,0)
,函数值
f(0,0)=2
。再考虑边界
x2+4y2=1
,使用拉格朗日乘数法,设
L(x,y,λ)=x2−y2+2−λ(x2+4y2−1)
。令偏导为零:
∂x∂L=2x−2λx=0,∂y∂L=−2y−2λy=0,∂λ∂L=x2+4y2−1=0.
由第一式得
x=0
或
λ=1
。若
x=0
,代入约束得
y=±2
,点
(0,2)
、
(0,−2)
,函数值
f=−2
。若
λ=1
,代入第二式得
y=0
,代入约束得
x=±1
,点
(1,0)
、
(−1,0)
,函数值
f=3
。
比较所有候选点函数值:
f(0,0)=2
,
f(0,±2)=−2
,
f(±1,0)=3
。故在椭圆域
D
上,最大值为 3,最小值为 -2。
21
(本题满分 9 分)
计算二重积分
∬Dx2+y2−1dσ
,
其中
D={(x,y)∣0≤x≤1,0≤y≤1}
【答案】
4π−31
【解析】
计算二重积分
∬Dx2+y2−1dσ
,其中
D=[0,1]×[0,1]
。由于被积函数有绝对值,需将区域
D
分为两部分:
D1={(x,y)∈D∣x2+y2≤1}
(四分之一单位圆盘)和
D2={(x,y)∈D∣x2+y2≥1}
(正方形减去四分之一圆盘)。在
D1
上,
x2+y2−1≤0
,故
x2+y2−1=1−x2−y2
;在
D2
上,
x2+y2−1≥0
,故
x2+y2−1=x2+y2−1
。积分化为:
∬Dx2+y2−1dσ=∬D1(1−x2−y2)dσ+∬D2(x2+y2−1)dσ. 首先计算
∬D1(1−x2−y2)dσ
。使用极坐标变换,令
x=rcosθ
,
y=rsinθ
,则
dσ=rdrdθ
,积分区域为
r∈[0,1]
,
θ∈[0,π/2]
。被积函数为
1−r2
,故:
∬D1(1−x2−y2)dσ=∫0π/2∫01(1−r2)rdrdθ.
先对
r
积分:
∫01(1−r2)rdr=∫01(r−r3)dr=[2r2−4r4]01=21−41=41.
再对
θ
积分:
∫0π/241dθ=41⋅2π=8π.
所以,
∬D1(1−x2−y2)dσ=8π
.
其次计算
∬D2(x2+y2−1)dσ
。利用积分可加性:
∬D2(x2+y2−1)dσ=∬D(x2+y2−1)dσ−∬D1(x2+y2−1)dσ.
计算
∬D(x2+y2−1)dσ
:
∬Dx2dσ=∫01∫01x2dydx=∫01x2dx⋅∫01dy=31⋅1=31,
∬Dy2dσ=∫01∫01y2dxdy=∫01y2dy⋅∫01dx=31⋅1=31,
∬D1dσ=1,
故:
∬D(x2+y2−1)dσ=31+31−1=−31.
计算
∬D1(x2+y2−1)dσ
,使用极坐标:
∬D1(x2+y2−1)dσ=∫0π/2∫01(r2−1)rdrdθ.
先对
r
积分:
∫01(r2−1)rdr=∫01(r3−r)dr=[4r4−2r2]01=41−21=−41.
再对
θ
积分:
∫0π/2−41dθ=−41⋅2π=−8π.
所以,
∬D1(x2+y2−1)dσ=−8π
。代入得:
∬D2(x2+y2−1)dσ=−31−(−8π)=−31+8π.
综上,原积分为:
∬Dx2+y2−1dσ=8π+(−31+8π)=4π−31. 22
(本题满分 9 分)
确定常数
a
,使向量组
α1=(1,1,a)T
,
α2=(1,a,1)T
,
α3=(a,1,1)T
可由向量组
β1=(1,1,a)T
,
β2=(−2,a,4)T
,
β3=(−2,a,a)T
线性表示,
但向量组
β1
,
β2
,
β3
不能由向量组
α1
,
α2
,
α3
线性表示.
【答案】
a=1
【解析】
记
A=(α1,α2,α3),B=(β1,β2,β3)
。由于
β1,β2,β3
不能由
α1,α2,α3
线性表示,故
r(A)<3
(若
r(A)=3
,则任何三维向量都可以由
α1,α2,α3
线性表示)。从而
∣A∣=11a1a1a11=−(2+a)(a−1)2=0, 从而得
a=1
或
a=−2
。
当
a=1
时,
α1=α2=α3=β1=(1,1,1)T
,则
α1=α2=α3=β1+0⋅β2+0⋅β3
,故
α1,α2,α3
可由
β1,β2,β3
线性表示,但
β2=(−2,1,4)T
不能由
α1,α2,α3
线性表示,故
a=1
符合题意。
当
a=−2
时,作初等行变换
(B:A)=11−2−2−24−2−2−2:::11−21−21−211→100−200−2−60:::10013−3−2−33 因
r(B)=2=r(B:α2)=3
,系数矩阵的秩和增广矩阵的秩不相等,故方程组
BX=α2
无解,即
α2
不能由
β1,β2,β3
线性表示,与题设矛盾。所以
a=−2
不合题意。
23
(本题满分 9 分)
同试卷 1 第 21 题