卷 2
填空题
本题共5小题,每小题3分,满分15分
1
设函数
f(x)={arcsin2x1−etanx,ae2x,x>0x≤0
在
x=0
处连续,则
a=
______.
【答案】
−2
【解析】
函数在
x=0
处连续,需满足左极限、右极限与函数值相等。
当
x≤0
时,
f(x)=ae2x
,故
f(0)=ae0=a
。
左极限为
limx→0−f(x)=limx→0−ae2x=a⋅1=a
。
右极限为
limx→0+f(x)=limx→0+arcsin2x1−etanx
。
当
x→0+
时,分子
1−etanx∼−tanx∼−x
,分母
arcsin2x∼2x
,因此
x→0+limf(x)∼2x−x=−2.
使用洛必达法则验证:
分子导数为
−etanxsec2x
,分母导数为
21⋅1−(2x)21
,
于是
x→0+limarcsin2x1−etanx=x→0+lim21⋅1−4x21−etanxsec2x=x→0+lim−etanxsec2x⋅21−4x2. 代入
x=0
,得
−1⋅1⋅2⋅1=−2
。
因此,右极限为
−2
。
由连续性,左极限、右极限与函数值相等,即
a=−2
。
2
位于曲线
y=xe−x(0≤x<+∞)
下方,
x
轴上方的无界图形的面积是 ______.
【答案】
1
【解析】
需要计算曲线
y=xe−x
(其中
0≤x<+∞
)下方、
x
轴上方的无界图形的面积,即计算积分
∫0∞xe−xdx
。
使用分部积分法:设
u=x
,
dv=e−xdx
,则
du=dx
,
v=−e−x
。代入分部积分公式:
∫xe−xdx=−xe−x−∫(−e−x)dx=−xe−x+∫e−xdx=−xe−x−e−x+C=−e−x(x+1)+C.
计算定积分:
∫0∞xe−xdx=b→∞lim[−e−x(x+1)]0b=b→∞lim[−e−b(b+1)−(−e0(0+1))]=b→∞lim[−e−b(b+1)+1].
当
b→∞
时,
e−b→0
,且
e−b(b+1)→0
,因此极限为 1。故积分值为 1,即所求面积为 1。
3
同试卷 1 第 3 题
4
limn→∞n1[1+cosnπ+1+cosn2π+⋯+1+cosnnπ]=
______.
【答案】
π22
【解析】
令
f(x)=1+cosx
,
Δxi=nπ
(
i=1,2,⋯,n
),由定积分的定义有
n→∞limn1[1+cosnπ+1+cosn2π+⋯+1+cosnnπ]=n→∞limπ1i=1∑n1+cosniπ⋅nπ=π1n→∞limi=1∑nf(niπ)Δxi=π1∫0π1+cosxdx=π2∫0πcos2xdx=π22. 5
矩阵
02−2−22−2−2−22
的非零特征值是 ______.
【答案】
4
【解析】
给定矩阵
A=02−2−22−2−2−22
,求其特征值。
计算特征多项式
det(A−λI)
:
A−λI=−λ2−2−22−λ−2−2−22−λ 展开行列式:
det(A−λI)=−λ⋅det(2−λ−2−22−λ)−(−2)⋅det(2−2−22−λ)+(−2)⋅det(2−22−λ−2)
计算各子式:
第一项:
−λ((2−λ)2−4)=−λ(λ2−4λ)=−λ3+4λ2
第二项:
2(2(2−λ)−4)=2(−2λ)=−4λ
第三项:
−2(−4+2(2−λ))=−2(−2λ)=4λ
求和:
det(A−λI)=(−λ3+4λ2)+(−4λ)+(4λ)=−λ3+4λ2=−λ2(λ−4)
特征方程为
−λ2(λ−4)=0
,解得特征值
λ=0
(重根)和
λ=4
。
非零特征值为
4
。
验证:矩阵的迹为
0+2+2=4
,特征值之和为
0+0+4=4
,吻合。
选择题
本题共5小题,每小题3分,共15分
6
设函数
f(u)
可导,
y=f(x2)
当自变量
x
在
x=−1
处取得增量
Δx=−0.1
时,
相应的函数增量
Δy
的线性主部为
0.1
,则
f′(1)=
正确答案:D【解析】
函数
y=f(x2)
的微分
dy
是函数增量
Δy
的线性主部。
根据链式法则,
dxdy=f′(x2)⋅2x,
因此
dy=f′(x2)⋅2x⋅dx.
当
x=−1
时,有
x2=1
,且
dx=Δx=−0.1
。代入得
dy=f′(1)⋅2⋅(−1)⋅(−0.1)=f′(1)⋅0.2.
已知
dy=0.1
,所以
0.1=f′(1)⋅0.2,
解得
f′(1)=0.20.1=0.5,
对应选项 D。
7
设函数
f(x)
连续,则下列函数中,必为偶函数的是
正确答案:D【解析】
对于选项A,设
g(x)=∫0xf(t2)dt
,则
g(−x)=∫0−xf(t2)dt
。令
u=−t
,得
g(−x)=−∫0xf(u2)du=−g(x)
,故
g(x)
为奇函数。
对于选项B,设
h(x)=∫0xf2(t)dt
,则
h(−x)=∫0−xf2(t)dt
。令
u=−t
,得
h(−x)=−∫0xf2(−u)du
。由于
f2(−u)
不一定等于
f2(u)
,故
h(−x)
不一定等于
h(x)
或
−h(x)
,因此
h(x)
不一定为偶函数。
对于选项C,设
k(x)=∫0xt[f(t)−f(−t)]dt
,则
k(−x)=∫0−xt[f(t)−f(−t)]dt
。令
u=−t
,得
k(−x)=−∫0xu[f(u)−f(−u)]du=−k(x)
,故
k(x)
为奇函数。
对于选项D,设
m(x)=∫0xt[f(t)+f(−t)]dt
,则
m(−x)=∫0−xt[f(t)+f(−t)]dt
。令
u=−t
,得
m(−x)=∫0xu[f(u)+f(−u)]du=m(x)
,故
m(x)
为偶函数。
因此,必为偶函数的是选项D。
8
设
y=(x)
是二阶常系数微分方程
y′′+py′+qy=e3x
满足初始条
y(0)=y′(0)=0
的特解,
则当
x→0
,函数
y(x)ln(1+x2)
的极限
正确答案:C【解析】
给定微分方程
y′′+py′+qy=e3x
满足初始条件
y(0)=y′(0)=0
,需要求极限
x→0limy(x)ln(1+x2).
当
x→0
时,
ln(1+x2)∼x2
,因此极限化为
x→0limy(x)x2.
由于
y(0)=0
和
y′(0)=0
,
y(x)
在
x=0
附近具有二阶零点,即
y(x)∼2y′′(0)x2.
代入微分方程在
x=0
处:
y′′(0)+py′(0)+qy(0)=e3⋅0=1,
利用初始条件得
y′′(0)=1
,因此
y(x)∼21x2.
于是
y(x)x2∼21x2x2=2,
极限为
2
。
9
同试卷 1 第 8 题
10
设向量组
α1,α2,α3
线性无关,向量
β1
可由
α1,α2,α3
线性表示,
而向量
β2
不能由
α1,α2,α3
线性表示,则对于任意常数
k
,必有
正确答案:A【解析】
已知向量组
α1,α2,α3
线性无关,
β1
可由
α1,α2,α3
线性表示,而
β2
不能由
α1,α2,α3
线性表示。
考虑选项 A 和 B 中的向量组
α1,α2,α3,kβ1+β2
。
由于
β1
可被
α1,α2,α3
线性表示,设
β1=c1α1+c2α2+c3α3,
则
kβ1+β2=k(c1α1+c2α2+c3α3)+β2.
若存在常数
a,b,c,d
使得
aα1+bα2+cα3+d(kβ1+β2)=0,
代入得
(a+dkc1)α1+(b+dkc2)α2+(c+dkc3)α3+dβ2=0.
因为
α1,α2,α3
线性无关,且
β2
不能由它们线性表示,所以
α1,α2,α3,β2
线性无关,因此系数必须为零:
d=0,
进而
a=0,b=0,c=0
。
故对于任意常数
k
,向量组
α1,α2,α3,kβ1+β2
线性无关,选项 A 正确。
对于选项 C 和 D,考虑向量组
α1,α2,α3,β1+kβ2
。
当
k=0
时,
β1+kβ2=β1
,由于
β1
可由
α1,α2,α3
线性表示,向量组线性相关;
当
k=0
时,向量组可能线性无关。
因此,对于任意常数
k
,该向量组不一定线性无关或线性相关,故选项 C 和 D 错误。
解答题
11
已知曲线的极坐标方程是
r=1−cosθ
,
求该曲线上对应于
θ=6π
处的切线与法线的直角坐标方程.
【答案】
切线方程:
4x−4y−33+5=0
或
y=x+45−33
法线方程:
4x+4y+1−3=0
或
y=−x+43−1
【解析】
由极坐标到直角坐标的变换公式
{x=rcosθy=rsinθ
得参数方程为
{x=(1−cosθ)cosθ,y=(1−cosθ)sinθ,⇒{x=cosθ−cos2θ,y=sinθ−cosθsinθ.
曲线上
θ=6π
的点对应的直角坐标为
切线斜率为
dxdyθ=6π=dθdxdθdyθ=6π=sinθ+2cosθsinθcosθ+sin2θ−cos2θθ=6π=1. 于是切线的直角坐标方程为
y−(21−43)=x−(23−43)⇒x−y−433+45=0. 法线的直角坐标方程为
y−(21−43)=−11(x−(23−43))⇒x+y−43+41=0. 12
设
f(x)={2x+23x2,(ex+1)2xex,−1≤x<0;0≤x≤1.
求函数
F(x)=∫−1xf(t)dt
的表达式.
【答案】
F(x)={x2+21x3−21,ex+1xex−ln(ex+1)+ln2−21,−1≤x<0;0≤x≤1.
【解析】
函数
F(x)=∫−1xf(t)dt
需根据
x
所在区间分段计算。
当
x∈[−1,0)
时,
f(t)=2t+23t2
,积分计算为:
∫−1x(2t+23t2)dt=[t2+21t3]−1x=(x2+21x3)−(1−21)=x2+21x3−21.
当
x∈[0,1]
时,积分分为两部分:
F(x)=∫−10f(t)dt+∫0xf(t)dt.
首先计算
∫−10f(t)dt
,其中
f(t)=2t+23t2
:
∫−10(2t+23t2)dt=[t2+21t3]−10=0−(1−21)=−21.
然后计算
∫0xf(t)dt
,其中
f(t)=(et+1)2tet
。使用分部积分,设
u=t
,
dv=(et+1)2etdt
,则
du=dt
,
v=−et+11
:
∫0x(et+1)2tetdt=[−et+1t]0x+∫0xet+11dt=−ex+1x+∫0xet+11dt.
计算
∫0xet+11dt
:
∫0xet+11dt=∫0x1+e−te−tdt=[−ln(1+e−t)]0x=−ln(1+e−x)+ln2.
代入得:
∫0x(et+1)2tetdt=−ex+1x−ln(1+e−x)+ln2.
简化
−ln(1+e−x)=x−ln(ex+1)
,且
−ex+1x+x=ex+1xex
,因此:
∫0x(et+1)2tetdt=ex+1xex−ln(ex+1)+ln2.
于是:
F(x)=−21+ex+1xex−ln(ex+1)+ln2.
在
x=0
处,两段表达式均得
F(0)=−21
,故连续。
13
已知函数
f(x)
在
(0,+∞)
内可导
f(x)>0
,
limx→+∞f(x)=1
,且满足
h→0lim(f(x)f(x+hx))h1=ex1,
求
f(x)
.
【答案】
f(x)=e−x1
【解析】
已知函数
f(x)
在
(0,+∞)
内可导,且
f(x)>0
,
limx→+∞f(x)=1
,并满足极限条件:
h→0lim(f(x)f(x+hx))h1=ex1.
对极限取自然对数:
ln[h→0lim(f(x)f(x+hx))h1]=x1.
由于对数函数连续,可交换极限与对数顺序:
h→0limh1ln(f(x)f(x+hx))=x1.
令
g(x)=lnf(x)
,则:
ln(f(x)f(x+hx))=g(x+hx)−g(x),
所以:
h→0limhg(x+hx)−g(x)=x1.
令
k=hx
,则当
h→0
时
k→0
,且
h=k/x
,代入得:
hg(x+hx)−g(x)=k/xg(x+k)−g(x)=x⋅kg(x+k)−g(x).
因此:
h→0limhg(x+hx)−g(x)=k→0limx⋅kg(x+k)−g(x)=xg′(x).
于是:
xg′(x)=x1⇒g′(x)=x21.
积分得:
g(x)=∫x21dx=−x1+C,
其中
C
为常数。由
g(x)=lnf(x)
,有:
lnf(x)=−x1+C⇒f(x)=e−x1+C=Ae−x1,
其中
A=eC>0
。利用条件
limx→+∞f(x)=1
:
x→+∞limAe−x1=A⋅1=1⇒A=1.
故
f(x)=e−x1
。验证满足原极限条件:
(f(x)f(x+hx))h1=(e−x1e−x+hx1)h1=eh1(−x(1+h)1+x1)=eh1⋅x1⋅1+hh=ex1⋅1+h1→ex1(h→0),
符合要求。因此,函数为
f(x)=e−x1
。
14
求微分方程
xdy+(x−2y)dx=0
的一个解
y=y(x)
,
使得由曲线
y=y(x)
与直线
x=1
,
x=2
以及
x
轴所围成的平面图形绕
x
轴旋转一周的旋转体体积最小.
【答案】
y=x−12475x2
【解析】
这是一阶线性微分方程
y′−x2y=−1
,由通解公式有
y=e∫x2dx[−∫e−∫x2dxdx+C]=x2[−∫x21dx+C]=x2(x1+C)=x+Cx2.
由曲线
y=x+Cx2
与
x=1,x=2
及
x
轴围成的图形绕
x
轴旋转一周的旋转体的体积为
V=π∫12(x+Cx2)2dx=π(531C2+215C+37).
求导并令导数为零,得到
dCdV=π(562C+215)=0.
解得
C=−12475
。又
V′′(C)>0
,故
C=−12475
为
V
的惟一极小值点,也是最小值点,于是所求曲线为
y=x−12475x2.
15
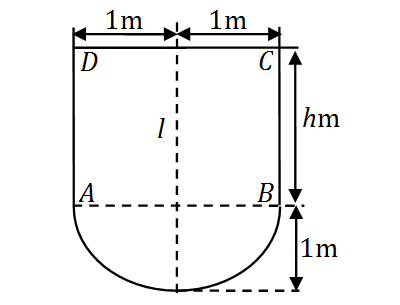
某闸门的形状与大小如图所示,其中直线
l
为对称轴,闸门的上部为矩形
ABCD
,下部由二次抛物线与线段
AB
所围成,
当水面与闸门的上端相平时,欲使闸门矩形部分承受的水压力与闸门下部承受的水压力之比为
5:4
,
闸门矩形部分的高
h
应为多少
m
(米)?
【答案】
2m
【解析】
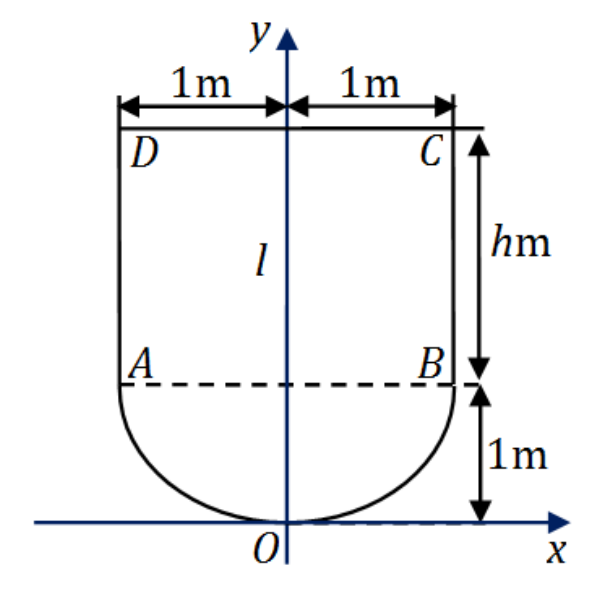
建立坐标系如下图:
设底部抛物线为
y=Px2+q
,由坐标轴的建立知此抛物线过
(0,0)
、
(1,1)
点,代入抛物线的方程,解得
q=0,P=1
,即底部抛物线是
y=x2(−1<x<1)
。
已知压力 = 压强 × 面积,设
ρ
为水的密度,
g
为重力加速度,则平板
ABCD
上所受的总压力为
P1=∫11+h2ρg(1+h−y)dy=ρgh2,
抛物板
AOB
上所受的总压力为
P2=∫012ρg(1+h−y)ydy=4ρg(31h+152). 由题意得
P1:P2=5:4⇒31h+152h2=45.
解之得
h=−31
(舍去)或
h=2
(米),即闸门矩形部分的高应为
2m
。
16
设
0<x1<3
,
xn+1=xn(3−xn)
(
n=1,2,⋯
),
证明数列
{xn}
的极限存在,并求此极限.
【答案】
23
【解析】
先说明有界性:由
0<x1<3
知
x1
及
3−x1
均为正数,故
0<x2=x1(3−x1)≤21(x1+3−x1)=23. 假设
0<xk≤23
(
k≥2
),则有
xk+1=xk(3−xk)≤21(xk+3−xk)=23. 由数学归纳法知,对任意正整数
n≥2
有
0<xn≤23
,即数列有界。
再说明单调性:因为
xn+1−xn=xn(3−xn)−xn≤xn(3−xn)+xnxn(3−xn)−xn2=xn(3−xn)+xnxn(3−2xn)≥0, 所以
{xn}
单调增加。
数列
{xn}
单调增加且有上界,所以
limn→∞xn
存在,记为
a
。
由
xn+1=xn(3−xn)
两边取极限得
a=a(3−a)
,即
2a2−3a=0
。解得
a=23
或
a=0
,但因
x1>0
且单调增加,故
a=0
,所以
limn→∞xn=23
。
17
设
0<a<b
,证明不等式
a2+b22a<b−alnb−lna<ab1
.
【解析】
设
t=ab>1
,则
b=at
。原不等式化为:
先证右边不等式
要证
t−1lnt<t1
,即证
lnt<tt−1
。
令
g(t)=tt−1−lnt
,则
g(1)=0
。
求导得:
g′(t)=2t3/2(t−1)2>0(t>1) 故
g(t)
在
t>1
时严格递增,所以
g(t)>0
,右边不等式成立。
再证左边不等式
要证
t−1lnt>1+t22
,即证
lnt>1+t22(t−1)
。
首先证明一个更强的结论:
lnt>t+12(t−1)
。
令
m(t)=lnt−t+12(t−1)
,则
m(1)=0
。
求导得:
m′(t)=t(t+1)2(t−1)2>0(t>1)
故
m(t)
在
t>1
时严格递增,所以
m(t)>0
,即
lnt>t+12(t−1)
。
当
t>1
时,有
t+1<1+t2
,因此:
t+12>1+t22
从而:
t−1lnt>t+12>1+t22
左边不等式成立。
综上,原不等式得证。
18
设函数
f(x)
在
x=0
的某邻域内具有二阶连续导数,且
f(0)=0
,
f′(0)=0
,
f′′(0)=0
.
证明:存在惟一的一组实数
λ1,λ2,λ3
,使得当
h→0
时,
λ1f(h)+λ2f(2h)+λ3f(3h)−f(0)
是比
h2
高阶的无穷小.
【解析】
由于
f(x)
在
x=0
的某邻域内具有二阶连续导数,可对
f(h)
、
f(2h)
、
f(3h)
在
x=0
处进行泰勒展开:
f(h)=f(0)+f′(0)h+2f′′(0)h2+o(h2),
f(2h)=f(0)+2f′(0)h+2f′′(0)h2+o(h2),
f(3h)=f(0)+3f′(0)h+29f′′(0)h2+o(h2).
代入表达式:
S=λ1f(h)+λ2f(2h)+λ3f(3h)−f(0),
得:
S=λ1[f(0)+f′(0)h+2f′′(0)h2]+λ2[f(0)+2f′(0)h+2f′′(0)h2]+λ3[f(0)+3f′(0)h+29f′′(0)h2]−f(0)+o(h2).
合并同类项:
- 常数项:
f(0)(λ1+λ2+λ3−1)
,
- 一阶项:
f′(0)h(λ1+2λ2+3λ3)
,
- 二阶项:
f′′(0)h2(2λ1+2λ2+29λ3)
.
为使
S=o(h2)
,需常数项、一阶项和二阶项系数均为零,即:
⎩⎨⎧λ1+λ2+λ3=1,λ1+2λ2+3λ3=0,2λ1+2λ2+29λ3=0. 将第三式乘以 2 得:
λ1+4λ2+9λ3=0.
解方程组:
由第一式和第二式相减得:
λ2+2λ3=−1
,
由第一式和第三式相减得:
3λ2+8λ3=−1
,
解得:
λ3=1
,
λ2=−3
,
λ1=3
。
此解唯一,且代入表达式后,
S
的泰勒展开中直至
h2
项系数为零,故
S=o(h2)
。
19
已知
A,B
为
3
阶矩阵,且满足
2A−1B=B−4E
,其中
E
是
3
阶单位矩阵.
(1) 证明:矩阵
A−2E
可逆;
(2) 若
B=110−220002
,求矩阵
A
.
【答案】
(1) 证明略(见解析)。
(2)
A=0−102−1000−2
【解析】
(Ⅰ) 由题设条件
2A−1B=B−4E
,两边左乘
A
,整理得
AB−2B−4A=0
。所以
(A−2E)(B−4E)=8E⇒(A−2E)⋅81(B−4E)=E.
根据可逆矩阵的定义知
A−2E
可逆,且
(A−2E)−1=81(B−4E)
。
(Ⅱ) 由 (Ⅰ) 结果知
A=8(B−4E)−1+2E
。而
B−4E=−310−2−2000−2⇒(B−4E)−1=−41−81041−83000−21 代入
A=8(B−4E)−1+2E
可得
A=8(B−4E)−1+2E=0−102−1000−2 20
同试卷 1 第 17 题