卷 1
填空题
本题共5小题,每小题3分,满分15分
1
设
y=ex(c1sinx+c2cosx)
(
c1,c2
为任意常数)为某二阶常系数线性齐次微分方程的通解,则该方程为 ______.
【答案】
y′′−2y′+2y=0
【解析】
给定通解
y=ex(c1sinx+c2cosx)
,可知该二阶常系数线性齐次微分方程的特征根为
r=1±i
。特征方程为
(r−(1+i))(r−(1−i))=0
,即
(r−1)2+1=0
,展开得
r2−2r+2=0
。因此,对应的微分方程为
y′′−2y′+2y=0
。
2
设
r=x2+y2+z2
,则
÷(∇r)∣(1,−2,2)=
______.
【答案】
32
【解析】
给定
r=x2+y2+z2
,需计算
÷(∇r)
在点
(1,−2,2)
的值。首先,计算梯度
∇r
:
∇r=(∂x∂r,∂y∂r,∂z∂r)=(rx,ry,rz).
然后计算散度:
÷(∇r)=∂x∂(rx)+∂y∂(ry)+∂z∂(rz).
对每一项求偏导:
∂x∂(rx)=r1−r3x2,∂y∂(ry)=r1−r3y2,∂z∂(rz)=r1−r3z2.
求和得:
÷(∇r)=(r1−r3x2)+(r1−r3y2)+(r1−r3z2)=r3−r3x2+y2+z2.
由于
x2+y2+z2=r2
,代入得:
÷(∇r)=r3−r3r2=r3−r1=r2.
在点
(1,−2,2)
处,计算
r=12+(−2)2+22=9=3
,因此:
÷(∇r)=32.
3
交换二次积分的积分次序:
∫−10dy∫21−yf(x,y)dx=
______.
【答案】
∫12dx∫1−x0f(x,y)dy
【解析】
原积分为
∫−10dy∫21−yf(x,y)dx
。积分区域由
y=−1
,
y=0
,
x=2
,和
x=1−y
围成。对于
y∈[−1,0]
,
x
从
1−y
到
2
(由于原积分中
x
从
2
到
1−y
,但上下限反转,因此实际区域为
x
从
1−y
到
2
)。
交换积分次序后,先积分
y
后积分
x
。确定
x
的范围:当
y=−1
时,
x=2
;当
y=0
时,
x=1
。因此
x
从
1
到
2
。对于固定
x∈[1,2]
,
y
的范围由
x=1−y
和
y=0
决定,即
y
从
1−x
到
0
。
因此,交换次序后的积分为
∫12dx∫1−x0f(x,y)dy
。
4
设矩阵
A
满足
A2
+A−4E=0
,其中
E
为单位矩阵,则
(A−E)−1
= ______.
【答案】
21(A+2E)
【解析】
已知矩阵
A
满足
A2+A−4E=0
,即
A2+A=4E.
考虑矩阵
(A−E)(A+2E)
,计算得
(A−E)(A+2E)=A2+2A−A−2E=A2+A−2E.
代入已知条件
A2+A=4E
,得
(A−E)(A+2E)=4E−2E=2E.
因此,
(A−E)(A+2E)=2E,
即
(A−E)⋅21(A+2E)=E.
故
(A−E)−1=21(A+2E).
5
设随机变量
X
的方差为
2
,则根据切比雪夫不等式有估计
P{∣X−E(X)∣≥2}≤
______.
【答案】
21
【解析】
切比雪夫不等式指出,对于随机变量
X
,若其期望为
E(X)
,方差为
σ2
,则对任意
k>0
,有:
P{∣X−E(X)∣≥k}≤k2σ2.
现已知方差
σ2=2
,取
k=2
,代入不等式可得:
P{∣X−E(X)∣≥2}≤222=42=21.
因此,所求概率上界为
21
。
选择题
本题共5小题,每小题3分,满分15分
6
设函数
f(x)
在定义域内可导,
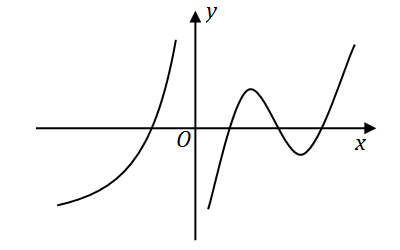
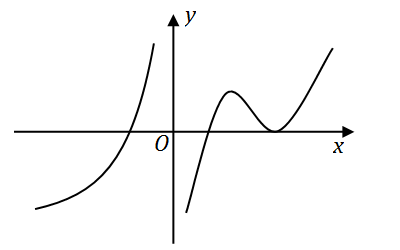
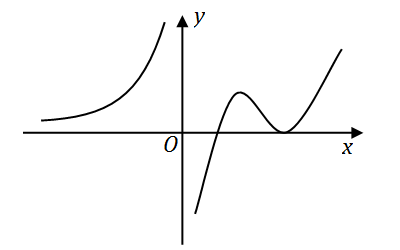
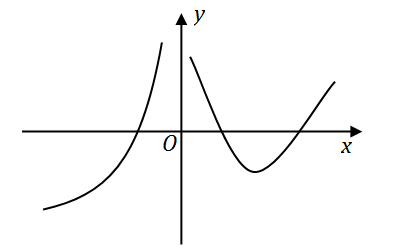
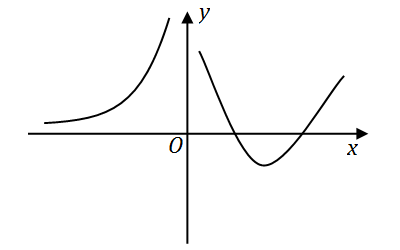
y=f(x)
的图形如下图所示,
则导函数
y=f′(x)
的图形为
正确答案:D
【解析】 应选 (D)。从题设图形可见,在
y
轴的左侧,曲线
y=f(x)
是严格单调增加的,因此当
x<0
时,一定有
f′(x)>0
,对应
y=f′(x)
图形必在
x
轴的上方,由此可排除 (A) 和 (C)。又
y=f(x)
的图形在
y
轴右侧靠近
y
轴部分单调增加,所以在这一段内一定有
f′(x)>0
,对应
y=f′(x)
图形必在
x
轴的上方,进一步可排除 (B),故正确答案为 (D)。
7
设函数
f(x,y)
在点
(0,0)
附近有定义,且
fx′(0,0)=3,fy′(0,0)=1
,则
正确答案:C【解析】
函数
f(x,y)
在点
(0,0)
处的偏导数为:
fx′(0,0)=3,fy′(0,0)=1.
考虑曲线
{z=f(x,y)y=0
该曲线位于平面
y=0
上,可参数化为:
x=t,y=0,z=f(t,0).
其切向量为:
(dtdx,dtdy,dtdz)=(1,0,fx(t,0)).
在点
(0,0,f(0,0))
处,即
t=0
,有
fx(0,0)=3
,因此切向量为:
(1,0,3).
✅ 选项 C 与此一致,正确。
❌ 选项 A 要求函数可微,但偏导数存在不一定保证可微,因此 A 不一定成立。
❌ 选项 B 中曲面
z=f(x,y)
的法向量应为:
(fx,fy,−1)=(3,1,−1),
而非
(3,1,1)
,因此 B 错误。
❌ 选项 D 给出的切向量为
(3,0,1)
,与计算结果
(1,0,3)
不符,因此 D 错误。
8
设
f(0)=0
,则
f(x)
在点
x=0
可导的充要条件为
正确答案:B【解析】
函数
f(x)
在
x=0
可导的充要条件是极限
h→0limhf(h)
存在(因为
f(0)=0
)。
分析选项 B:
h→0limh1f(1−eh)
令
u=1−eh
,则当
h→0
时,
u→0
,且
h∼−u
。于是
h1f(1−eh)∼−u1f(u)=−uf(u).
因此该极限存在当且仅当
u→0limuf(u)
存在,即
f(x)
在
x=0
可导。故选项 B 是充要条件。
分析选项 A:
h→0limh21f(1−cosh)
取
f(x)=∣x∣
,则
f(0)=0
,但
f(x)
在
x=0
不可导。计算极限:
h21f(1−cosh)=h21∣1−cosh∣=h21(1−cosh)→21,
极限存在,但
f(x)
不可导,因此 A 不是充要条件。
分析选项 C:
h→0limh21f(h−sinh)
取
f(x)=∣x∣2/3
,则
f(0)=0
,但
f(x)
在
x=0
不可导。计算极限:
h21f(h−sinh)≈h216h32/3=h21⋅62/3h2=62/31, 极限存在,但
f(x)
不可导,因此 C 不是充要条件。
分析选项 D:
h→0limh1[f(2h)−f(h)]
取
f(x)=1
(当
x=0
)且
f(0)=0
,则
f(x)
在
x=0
不连续,故不可导。计算极限:
h1[f(2h)−f(h)]=h1[1−1]=0,
极限存在,但
f(x)
不可导,因此 D 不是充要条件。
结论: 唯一充要条件为选项 B。
9
设
A=1111111111111111,B=4000000000000000
,则
A
与
B
正确答案:A【解析】
因为
A
是实对称矩阵,故
A
必相似于一对角阵
Λ
。又由相似矩阵有相同的特征值,相同的秩,知
A
与
Λ
有相同的秩,故
r(Λ)=r(A)=1
,即
Λ
对角线上有 3 个元素为零。因此,
λ1=λ2=λ3=0
是
A
的特征值。由特征值的和等于矩阵主对角线元素之和,知
i=1∑4λi=λ4=i=1∑4aii=4.
故
λ4=4
。即
A
有特征值
λ=4
和
λ=0
(三重根),和对角阵
B
的特征值完全一致,故
A,B
相似。又由两矩阵合同的充要条件:实对称矩阵
A
与
B
合同的充要条件是
A
与
B
相似。知
A,B
合同。
10
将一枚硬币重复掷
n
次,以
X
和
Y
分别表示正面向上和反面向上的次数,则
X
和
Y
的相关系数等于
正确答案:A【解析】
每次掷硬币的结果为正面或反面,设正面次数为
X
,反面次数为
Y
,则满足
X+Y=n,
即
Y=n−X.
因此,
X
与
Y
存在完全的线性负相关关系。
计算协方差:
Cov(X,Y)=Cov(X,n−X)=−Var(X).
方差满足:
Var(Y)=Var(n−X)=Var(X).
因此,相关系数为
ρ=σXσYCov(X,Y)=Var(X)⋅Var(X)−Var(X)=−1. 故答案为 A。
解答题
11
∫e2xarctanexdx=
【答案】
−21e−x−21arctanex(1+e−2x)+C
【解析】
考虑积分
I=∫e2xarctanexdx
。令
u=ex
,则
du=exdx
,即
dx=udu
。代入得:
I=∫u2arctanu⋅udu=∫u3arctanudu.
使用分部积分法,令
p=arctanu
,
dq=u−3du
,则
dp=1+u21du
,
q=−21u−2
。于是:
∫pdq=pq−∫qdp=−21u−2arctanu+21∫1+u2u−2du.
计算积分
∫1+u2u−2du=∫u2(1+u2)1du
。进行部分分式分解:
u2(1+u2)1=u21−1+u21,
所以:
∫u2(1+u2)1du=∫u21du−∫1+u21du=−u1−arctanu+C.
代回得:
∫u3arctanudu=−21u−2arctanu+21(−u1−arctanu)+C=−21u−2arctanu−21u−1−21arctanu+C.
将
u=ex
代回,得到:
I=−21e−2xarctanex−21e−x−21arctanex+C=−21e−x−21arctanex(1+e−2x)+C.
此为最终结果。
12
设函数
z=f(x,y)
在点(1,1) 处可微,且
f(1,1)=1,∂x∂f(1,1)=2,∂y∂f(1,1)=3,φ(x)=f(x,f(x,x)). 求
dxdφ3(x)x=1
.
【答案】
51
【解析】
给定函数
φ(x)=f(x,f(x,x))
,需要求
dxdφ3(x)x=1
。首先,计算
dxdφ3(x)=3[φ(x)]2φ′(x)
,因此需要求
φ(1)
和
φ′(1)
。
由已知条件,
f(1,1)=1
,所以
φ(1)=f(1,f(1,1))=f(1,1)=1
。
接下来,求
φ′(x)
。令
u=x
,
v=f(x,x)
,则
φ(x)=f(u,v)
。由链式法则:
φ′(x)=∂u∂f⋅dxdu+∂v∂f⋅dxdv
其中
dxdu=1
,而
dxdv=dxdf(x,x)=∂x∂f(x,x)+∂y∂f(x,x)
。
在
x=1
时,点
(u,v)=(1,f(1,1))=(1,1)
,因此:
∂u∂f(1,1)=∂x∂f(1,1)=2,∂v∂f(1,1)=∂y∂f(1,1)=3 且
dxdvx=1=∂x∂f(1,1)+∂y∂f(1,1)=2+3=5 所以:
φ′(1)=2⋅1+3⋅5=2+15=17
代入:
dxdφ3(x)x=1=3[φ(1)]2φ′(1)=3⋅12⋅17=51 因此,结果为 51。
13
设
f(x)={x1+x2arctanx,1,x=0;x=0.
试将
f(x)
展开成
x
的幂级数,并求级数
∑n=1∞1−4n2(−1)n
的和.
【答案】
n=1∑∞1−4n2(−1)n=4π−21
【解析】
给定函数
f(x)={x1+x2arctanx,1,x=0;x=0.
将其展开为
x
的幂级数。
首先,对于
x=0
,有:
f(x)=x1+x2arctanx=xarctanx+xarctanx.
利用
arctanx
的麦克劳林级数:
arctanx=n=0∑∞(−1)n2n+1x2n+1,∣x∣<1,
代入得:
xarctanx=n=0∑∞(−1)n2n+1x2n,xarctanx=n=0∑∞(−1)n2n+1x2n+2.
因此,
f(x)=n=0∑∞(−1)n2n+1x2n+n=0∑∞(−1)n2n+1x2n+2.
将第二个级数改写为:
n=0∑∞(−1)n2n+1x2n+2=m=1∑∞(−1)m−12m−1x2m.
于是,
f(x)=1+n=1∑∞(−1)n2n+1x2n+n=1∑∞(−1)n−12n−1x2n=1+n=1∑∞[(−1)n2n+11+(−1)n−12n−11]x2n.
简化括号内表达式:
(−1)n2n+11+(−1)n−12n−11=(−1)n(2n+11−2n−11)=(−1)n⋅4n2−1−2=4n2−12(−1)n+1.
因此,
f(x)=1+n=1∑∞4n2−12(−1)n+1x2n.
这就是
f(x)
的幂级数展开。
现在求级数
∑n=1∞1−4n2(−1)n
的和。注意到:
1−4n2(−1)n=−(4n2−1)(−1)n=−4n2−1(−1)n=4n2−1(−1)n+1.
在
f(x)
的展开式中,令
x=1
,有:
f(1)=11+12arctan1=2⋅4π=2π,
同时由级数展开:
f(1)=1+n=1∑∞4n2−12(−1)n+1.
所以,
2π=1+n=1∑∞4n2−12(−1)n+1,
即:
n=1∑∞4n2−12(−1)n+1=2π−1,
因此:
n=1∑∞4n2−1(−1)n+1=4π−21.
于是,
n=1∑∞1−4n2(−1)n=n=1∑∞4n2−1(−1)n+1=4π−21.
14
计算
I=∮L(y2−z2)dx+(2z2−x2)dy+(3x2−y2)dz
,
其中
L
是平面
x+y+z=2
与柱面
∣x∣+∣y∣=1
的交线,从
z
轴正向看去,
L
为逆时针方向.
【答案】
−24
【解析】
使用斯托克斯定理将曲线积分转化为曲面积分。给定向量场
F=(P,Q,R)=(y2−z2,2z2−x2,3x2−y2)
,计算旋度:
∇×F=(∂y∂R−∂z∂Q,∂z∂P−∂x∂R,∂x∂Q−∂y∂P)=(−2y−4z,−2z−6x,−2x−2y).
曲线
L
是平面
x+y+z=2
与柱面
∣x∣+∣y∣=1
的交线,选取曲面
S
为平面
x+y+z=2
上被
L
包围的部分。参数化曲面为
z=2−x−y
,其中
(x,y)
在区域
D:∣x∣+∣y∣≤1
上。曲面向量元为
dS=(1,1,1)dxdy
,方向与从
z
轴正向看逆时针方向一致。
曲面积分为:
∬S(∇×F)⋅dS=∬D(∇×F)⋅(1,1,1)dxdy.
计算点积:
(∇×F)⋅(1,1,1)=(−2y−4z)+(−2z−6x)+(−2x−2y)=−8x−4y−6z.
代入
z=2−x−y
:
−8x−4y−6(2−x−y)=−8x−4y−12+6x+6y=−2x+2y−12.
因此,积分化为:
∬D(−2x+2y−12)dxdy.
区域
D
是菱形
∣x∣+∣y∣≤1
,关于
x
轴和
y
对称。函数
−2x
和
2y
是奇函数,积分值为零。常数项
−12
的积分为:
−12×Area(D)=−12×2=−24.
故曲线积分
I=−24
。
\boxed{-24}
15
设
y=f(x)
在
(−1,1)
内具有二阶连续导数且
f′′(x)=0
,试证:
(1) 对于
(−1,1)
内的任意
x=0
,存在唯一的
θ(x)∈(0,1)
,
使得
f(x)=f(0)+xf′(θ(x)x)
成立;
(2)
limx→0θ(x)=21
.
【答案】
(1) 对于任意
x=0
在
(−1,1)
内,存在唯一的
θ(x)∈(0,1)
使得
f(x)=f(0)+xf′(θ(x)x)
成立。
(2)
limx→0θ(x)=21
。
【解析】
(1) 由拉格朗日中值定理,对于
x=0
在
(−1,1)
内,存在
c
在
0
与
x
之间使得
f(x)−f(0)=f′(c)x
。令
c=θ(x)x
,则
θ(x)=c/x
。当
x>0
时,
c∈(0,x)
,故
θ(x)∈(0,1)
;当
x<0
时,
c∈(x,0)
,故
θ(x)∈(0,1)
。因此存在
θ(x)∈(0,1)
满足等式。
为证唯一性,考虑
f′′(x)=0
且连续,故
f′′(x)
恒正或恒负,从而
f′(x)
严格单调。对于固定
x
,函数
h(θ)=f′(θx)
是严格单调的,因此方程
h(θ)=xf(x)−f(0)
有唯一解
θ∈(0,1)
。故
θ(x)
唯一。
(2) 由泰勒展开,在
x=0
处有:
f(x)=f(0)+f′(0)x+21f′′(0)x2+o(x2)
又由给定等式:
f(x)=f(0)+xf′(θx)
对
f′(θx)
在
0
处展开:
f′(θx)=f′(0)+f′′(0)θx+o(θx)=f′(0)+f′′(0)θx+o(x)
代入得:
f(x)=f(0)+x[f′(0)+f′′(0)θx+o(x)]=f(0)+f′(0)x+f′′(0)θx2+o(x2)
比较两式:
f(0)+f′(0)x+f′′(0)θx2+o(x2)=f(0)+f′(0)x+21f′′(0)x2+o(x2)
即:
f′′(0)θx2+o(x2)=21f′′(0)x2+o(x2)
整理得:
f′′(0)(θ−21)x2=o(x2)
由于
f′′(0)=0
,两边除以
f′′(0)x2
:
θ−21=f′′(0)x2o(x2)→0(x→0)
故
limx→0θ(x)=21
。
16
设有一高度为
h(t)
(
t
为时间)的雪堆在融化过程中,其侧面满足方程
z=h(t)−h(t)2(x2+y2)
(设长度单位为厘米,时间单位为小时),已知体积减少的速率与侧面积成正比(比例系数
0.9
),
问高度为
130
厘米的雪堆全部融化需多少小时?
【答案】
100
【解析】
雪堆的形状由方程
z=h(t)−h(t)2(x2+y2)
描述,这是一个旋转抛物面。首先,计算体积
V
和侧面积
S
作为
h(t)
的函数。
体积
V
通过积分求得:
在高度
z
处的截面半径满足
r2=2h(h−z)
,因此
V=∫0hπr2dz=∫0hπ⋅2h(h−z)dz=π2h∫0h(h−z)dz=π2h⋅2h2=4πh3
侧面积
S
通过旋转曲面积分求得:
由曲线
z=h−h2r2
,其中
r
从
0
到
2h
,
drdz=−h4r
S=∫02h2πr1+(drdz)2dr=∫02h2πr1+h216r2dr 令
u=h4r
,则
dr=4hdu
,积分限变为
u=0
到
u=22
,
S=∫0222π(4hu)1+u2⋅4hdu=8πh2∫022u1+u2du 计算积分:令
v=1+u2
,则
dv=2udu
,
∫022u1+u2du=21∫19v1/2dv=21⋅32v3/219=31(27−1)=326 因此,
S=8πh2⋅326=1213πh2
已知体积减少速率与侧面积成正比,比例系数
0.9
,即
dtdV=−0.9S
代入
V
和
S
:
dtd(4πh3)=−0.9⋅1213πh2
求导得:
43πh2dtdh=−0.9⋅1213πh2
两边除以
πh2
(假设
h=0
):
43dtdh=−0.9⋅1213
计算右边:
0.9⋅1213=109⋅1213=120117=4039
所以,
43dtdh=−4039
解得:
dtdh=−4039⋅34=−1013
即高度减少速率为常数
−1013
cm/h。
雪堆初始高度为 130 cm,全部融化时高度为 0,所需时间为:
t=1013130=130⋅1310=100
因此,雪堆全部融化需 100 小时。
17
设
α1,α2,⋯,αs
为线性方程组
Ax=0
的一个基础解系,
β1=t1α1+t2α2,β2=t1α2+t2α3,⋯,βs=t1αs+t2α1,
其中
t1,t2
为实常数.试问
t1,t2
满足什么关系时,
β1,β2,⋯,βs
也为
Ax=0
的一个基础解系?
【答案】
当
s
为奇数时,
t1+t2=0
;当
s
为偶数时,
t1+t2=0
且
t1−t2=0
。
【解析】
设
α1,α2,⋯,αs
是线性方程组
Ax=0
的一个基础解系,则它们线性无关且张成解空间。
β1,β2,⋯,βs
是
α1,α2,⋯,αs
的线性组合,因此每个
βi
都是
Ax=0
的解。要使
β1,β2,⋯,βs
也成为基础解系,只需它们线性无关。
考虑变换矩阵
T
,使得
[β1,β2,⋯,βs]=[α1,α2,⋯,αs]T
,其中
T
是
s×s
矩阵:
T=t1t20⋮000t1t2⋮0000t1⋮00⋯⋯⋯⋱⋯⋯000⋮t1t2t200⋮0t1. 由于
α1,α2,⋯,αs
线性无关,
β1,β2,⋯,βs
线性无关当且仅当
T
可逆。
矩阵
T
可以写为
T=t1I+t2P
,其中
P
是循环置换矩阵:
P=010⋮00001⋮00000⋮00⋯⋯⋯⋱⋯⋯000⋮01100⋮00. P
的特征值为
ωk
(
k=0,1,…,s−1
),其中
ω=e2πi/s
。因此
T
的特征值为
t1+t2ωk
(
k=0,1,…,s−1
)。
T
可逆当且仅当所有特征值非零,即
t1+t2ωk=0
对所有
k
成立。
当
t2=0
时,
T=t1I
,可逆当且仅当
t1=0
。当
t2=0
时,条件等价于
−t1/t2
不是
s
次单位根。考虑到
t1,t2
为实数,仅需考虑实单位根:
- 若
s
为奇数,实单位根只有
1
,故需
t1+t2=0
。
- 若
s
为偶数,实单位根有
1
和
−1
,故需
t1+t2=0
且
t1−t2=0
。
当
s=1
时,
β1=(t1+t2)α1
,线性无关当且仅当
t1+t2=0
,与奇数情况一致。
因此,综上所述,当
s
为奇数时,条件为
t1+t2=0
;当
s
为偶数时,条件为
t1+t2=0
且
t1−t2=0
。
18
已知
3
阶矩阵
A
与三维向量
x
,使得向量组
x,Ax,A2x
线性无关,且满足
A3x=3Ax−2A2x.
(1) 记
P=(x,Ax,A2x)
,求
3
阶矩阵
B
,使
A=PBP−1
;
(2) 计算行列式
∣A+E∣
.
【答案】
B=01000103−2,∣A+E∣=−4 【解析】
已知向量组
x,Ax,A2x
线性无关,且满足
A3x=3Ax−2A2x
。令
P=(x,Ax,A2x)
,则
P
可逆。
(1) 求矩阵
B
使得
A=PBP−1
。考虑基向量
v1=x
,
v2=Ax
,
v3=A2x
,计算
A
在这些基向量上的作用:
- Av1=Ax=v2
,对应坐标
(0,1,0)T
;
- Av2=A(Ax)=A2x=v3
,对应坐标
(0,0,1)T
;
- Av3=A(A2x)=A3x=3Ax−2A2x=3v2−2v3
,对应坐标
(0,3,−2)T
。
因此,矩阵
B
为:
B=01000103−2
(2) 计算行列式
∣A+E∣
。由
A=PBP−1
,得
A+E=PBP−1+PIP−1=P(B+I)P−1
,故
∣A+E∣=∣P(B+I)P−1∣=∣B+I∣
。计算
B+I
:
行列式为:
∣B+I∣=11001103−1=1⋅113−1=1⋅(1⋅(−1)−3⋅1)=−4 因此,
∣A+E∣=−4
。
19
设某班车起点站上客人数
X
服从参数
λ
(
λ>0
)的泊松分布,
每位乘客在中途下车的概率为
p
(
0<p<1
),且途中下车与否相互独立,以
Y
表示在中途下车的人数,求:
(1) 在发车时有
n
个乘客的条件下,中途有
m
人下车的概率;
(2) 二维随机变量
(X,Y)
的概率分布.
【答案】
(1) 在发车时有
n
个乘客的条件下,中途有
m
人下车的概率为:
P(Y=m∣X=n)=(mn)pm(1−p)n−m,m=0,1,…,n.
(2) 二维随机变量
(X,Y)
的概率分布为:
对于
n=0,1,2,…
和
m=0,1,…,n
,
P(X=n,Y=m)=(mn)pm(1−p)n−m⋅n!λne−λ.
当
n<m
时,
P(X=n,Y=m)=0
。
【解析】
(1) 给定发车时乘客人数
X=n
,每位乘客中途下车相互独立且概率为
p
,因此中途下车人数
Y
服从二项分布,即
P(Y=m∣X=n)=(mn)pm(1−p)n−m.
(2) 二维随机变量
(X,Y)
的联合概率分布可通过条件概率公式得到:
P(X=n,Y=m)=P(Y=m∣X=n)⋅P(X=n).
其中
P(X=n)
是参数为
λ
的泊松分布,即
P(X=n)=n!λne−λ,
而
P(Y=m∣X=n)
如 (1) 所示。
因此,当
n≥m
时,有
P(X=n,Y=m)=(mn)pm(1−p)n−m⋅n!λne−λ;
当
n<m
时,概率为
0
。
20
设总体
X
服从正态分布
N(μ,σ2)
(
σ>0
),
从该总体中抽取简单随机样本
X1
,
X2
,
⋯
,
X2n
(
n≥2
),
其样本均值为
X=2n1∑i=12nXi
,求统计量
Y=i=1∑n(Xi+Xn+i−2X)2
的数学期望
E(Y)
.
【答案】
2(n−1)σ2
【解析】
设
Si=Xi+Xn+i
,则
Si∼N(2μ,2σ2)
,且
S1,S2,…,Sn
相互独立。
样本均值为
X=2n1i=1∑2nXi=2n1i=1∑nSi,
因此
2X=n1i=1∑nSi=Sˉ,
其中
Sˉ
是
Si
的样本均值。
定义统计量
Y=i=1∑n(Si−Sˉ)2.
由于
Si
独立同分布,且
Sˉ
为其样本均值,有
E[i=1∑n(Si−Sˉ)2]=(n−1)Var(Si).
已知
Var(Si)=2σ2
,故
E(Y)=(n−1)⋅2σ2=2(n−1)σ2.