卷 3
填空题
本题共5分,每小题3分,满分15分
1
设
y=f(lnx)ef(x)
,其中
f
可微,则
dy=
______.
【答案】
dy=ef(x)[f(lnx)f′(x)+x1f′(lnx)]dx
【解析】
给定
y=f(lnx)⋅ef(x)
,其中
f
可微。
设
u=f(lnx),v=ef(x),
则
y=u⋅v.
由乘积法则,
dxdy=udxdv+vdxdu.
计算
dxdu
:
dxdu=f′(lnx)⋅dxd(lnx)=f′(lnx)⋅x1.
计算
dxdv
:
dxdv=ef(x)⋅f′(x).
代入乘积法则:
dxdy=f(lnx)⋅ef(x)f′(x)+ef(x)⋅(f′(lnx)⋅x1)=ef(x)[f(lnx)f′(x)+x1f′(lnx)].
因此,
dy=dxdydx=ef(x)[f(lnx)f′(x)+x1f′(lnx)]dx.
2
若
f(x)=1+x21+1−x2∫01f(x)dx
,则
∫01f(x)dx=
______.
【答案】
4−ππ
【解析】
设
I=∫01f(x)dx
,则原方程化为:
对两边从 0 到 1 积分:
I=∫011+x21dx+I∫011−x2dx 计算第一个积分:
∫011+x21dx=arctanx01=4π 计算第二个积分:
代入得:
I=4π+I⋅4π
整理方程:
I−4πI=4π
I(1−4π)=4π
解得:
I=1−4π4π=4π⋅4−π4=4−ππ
因此,
∫01f(x)dx=4−ππ
。
3
差分方程
yt+1−yt=t2t
的通解为 ______.
【答案】
yt=C+(t−2)2t
【解析】
给定差分方程
yt+1−yt=t2t
,首先求解齐次方程
yt+1−yt=0
。
齐次方程的特征方程为
r−1=0
,解得
r=1
,因此齐次解为
yh=C
,其中
C
为常数。
接下来,求非齐次方程的特解。非齐次项为
t2t
,假设特解形式为
yp=(At+B)2t
。代入原方程:
yp,t+1=(A(t+1)+B)2t+1=2(At+A+B)2t,
则
yp,t+1−yp=2(At+A+B)2t−(At+B)2t=[At+(2A+B)]2t.
令其等于
t2t
,得
At+(2A+B)=t.
比较系数:
解得
B=−2
。
因此特解为
yp=(t−2)2t
。
通解为齐次解与特解之和:
yt=yh+yp=C+(t−2)2t.
4
若二次型
f(x1,x2,x3)=2x12+x22+x32+2x1x2+tx2x3
是正定的,则
t
的取值范围是 ______.
【答案】
−2<t<2
【解析】
二次型
f(x1,x2,x3)=2x12+x22+x32+2x1x2+tx2x3
的矩阵为:
二次型正定的充要条件是矩阵
A
的所有顺序主子式大于零。
一阶主子式:
2>0
。
二阶主子式:
2111=2×1−1×1=1>0
。
三阶主子式:
210112t02t1=2×12t2t1−1×102t1=2(1−4t2)−1=1−2t2
。
要求
1−2t2>0
,即
t2<2
,所以
−2<t<2
。
因此,
t
的取值范围是
−2<t<2
。
5
设随机变量
X
和
Y
相互独立且都服从正态分布
N(0,32)
,
而
X1,⋯,X9
和
Y1,⋯,Y9
分别是来自总体
X
和
Y
的简单随机样本,
则统计量
U=Y12+⋯+Y92X1+⋯+X9
服从分布______,参数为 ______.
【答案】 t分布;9
【解析】 由于
X
和
Y
相互独立且均服从
N(0,32)
,则
Xi∼N(0,9)
,
Yi∼N(0,9)
。
分子
SX=∑i=19Xi
服从正态分布,
SX∼N(0,9×9)=N(0,81)
,标准化后
9SX∼N(0,1)
。
分母涉及
Yi
的平方和:令
Zi=3Yi∼N(0,1)
,则
i=1∑9Zi2=i=1∑9(3Yi)2=91i=1∑9Yi2,
故
i=1∑9Yi2=9i=1∑9Zi2∼9χ2(9),
因此
统计量
U=∑Yi2SX=3χ2(9)9⋅N(0,1)=3⋅χ2(9)N(0,1)=3⋅39χ2(9)N(0,1)=9χ2(9)N(0,1). 由于分子
9SX∼N(0,1)
与分母中的
χ2(9)
相互独立,故
U∼t(9)
,即服从自由度为 9 的 t 分布。
选择题
本题共5小题,每小题3分,满分15分
6
设
f(x)=∫01−cosxsint2dt
,
g(x)=5x5+6x6
,
则当
x→0
时,
f(x)
是
g(x)
的
正确答案:B【解析】 当
x→0
时,分析
f(x)
和
g(x)
的阶数。首先,
g(x)=5x5+6x6∼5x5
,因为
x6
项是高阶无穷小。对于
f(x)=∫01−cosxsint2dt,
令
u=1−cosx
。当
x→0
时,
u∼2x2
。被积函数
sint2
在
t→0
时满足
sint2∼t2
,因此
f(x)∼∫0ut2dt=3u3∼31(2x2)3=24x6.
比较
f(x)∼24x6
和
g(x)∼5x5
,有
g(x)f(x)∼5x524x6=245x→0,
故
f(x)
是
g(x)
的高阶无穷小。
7
若
f(−x)=f(x)
(
−∞<x<+∞
),在
(−∞,0)
内
f′(x)>0
,且
f′′(x)<0
,则在
(0,+∞)
内有
正确答案:C【解析】
由条件
f(−x)=f(x)
可知函数
f(x)
是偶函数。
对于偶函数,一阶导数
f′(x)
是奇函数,即
f′(−x)=−f′(x)
在
(−∞,0)
内
f′(x)>0
,则对于
x>0
,有
f′(−x)>0
,即
−f′(x)>0
所以
f′(x)<0
二阶导数
f′′(x)
是偶函数,即
f′′(−x)=f′′(x)
在
(−∞,0)
内
f′′(x)<0
,则对于
x>0
,有
f′′(x)=f′′(−x)<0
因此在
(0,+∞)
内
f′(x)<0且f′′(x)<0
对应选项 C。
8
设向量组
α1
,
α2
,
α3
线性无关,则下列向量组中,线性无关的是
正确答案:C【解析】
由于向量组
α1,α2,α3
线性无关,要判断各选项向量组的线性相关性,需设其线性组合为零,并解系数方程组。
对于选项 C,设
c1(α1+2α2)+c2(2α2+3α3)+c3(3α3+α1)=0,
整理得
(c1+c3)α1+(2c1+2c2)α2+(3c2+3c3)α3=0.
由
α1,α2,α3
线性无关,得方程组:
c1+c3=0,2c1+2c2=0,3c2+3c3=0.
解得
c1=0, c2=0, c3=0
,故线性无关。
对于选项 A,方程组有非零解,如
c1=1, c2=−1, c3=1
;
选项 B 有非零解,如
c1=1, c2=1, c3=−1
;
选项 D 有非零解,如
c1=−19, c2=2, c3=5
,
故这些选项线性相关。
9
设
A,B
为同阶可逆矩阵,则
正确答案:D【解析】
对于选项 A,矩阵乘法不满足交换律,因此
AB=BA
不一定成立,例如取
A=[1011],B=[1101],
则
AB=BA
。
对于选项 B,
A
与
B
相似要求它们有相同的特征值,但
A
和
B
可能特征值不同,例如
A=[1002],B=[1003]
不相似。
对于选项 C,存在可逆矩阵
C
使
CTAC=B
要求
A
与
B
合同,但
A
和
B
可能不合同,例如在实数域中
A=[1001],B=[100−1],
由于
CTAC
总是正定或半正定,而
B
是负定,不可能相等。
对于选项 D,由于
A
和
B
都是同阶可逆矩阵,它们有相同的秩(满秩),因此存在可逆矩阵
P
和
Q
使得
PAQ=B
,即
A
与
B
等价,例如取
P=BA−1
和
Q=I
,则
PAQ=B
。
10
设两个随机变量
X
与
Y
相互独立且同分布:
P{X=−1}=P{Y=−1}=21,P{X=1}=P{Y=1}=21,
则下列各式中成立的是
正确答案:A【解析】
由于随机变量
X
与
Y
相互独立且同分布,且
P{X=−1}=P{Y=−1}=21,P{X=1}=P{Y=1}=21,
可计算各选项概率。
对于选项 A:
P{X=Y}
表示
X
与
Y
取值相同,即
X=−1
且
Y=−1
或
X=1
且
Y=1
。由于独立,
P{X=−1,Y=−1}=21×21=41,P{X=1,Y=1}=21×21=41,
因此
P{X=Y}=41+41=21,
选项 A 正确。
对于选项 B:
P{X=Y}=1
显然错误,因为存在
X=Y
的情况。
对于选项 C:
P{X+Y=0}
表示
X
与
Y
取值相反,即
X=−1
且
Y=1
或
X=1
且
Y=−1
。
P{X=−1,Y=1}=21×21=41,P{X=1,Y=−1}=21×21=41,
因此
P{X+Y=0}=41+41=21=41,
选项 C 错误。
对于选项 D:
P{XY=1}
表示
X
与
Y
同号,即
X=−1
且
Y=−1
或
X=1
且
Y=1
。与选项 A 相同,
P{XY=1}=41+41=21=41,
选项 D 错误。
因此,唯一成立的选项是 A。
解答题
11
在经济学中,称函数
Q(x)=A[δK−x+(1−δ)L−x]−x1
为固定替代弹性生产函数,
而称函数
Q=AKδL1−δ
为 Cobb-Douglas 生产函数(简称 C-D 生产函数)。
试证明:当
x→0
时,固定替代弹性生产函数变为 C-D 生产函数,即有
limx→0Q(x)=Q
.
【答案】 见解析
【解析】
因为
lnQ(x)=lnA−x1ln[δK−x+(1−δ)L−x]
,而且
x→0limxln[δK−x+(1−δ)L−x]=x→0limδK−x+(1−δ)L−x−δK−xlnK−(1−δ)L−xlnL=−δlnK−(1−δ)lnL=−ln(KδL1−δ),
所以
x→0limlnQ(x)=lnA+ln(KδL1−δ)=ln(AKδL1−δ)⟹x→0limQ(x)=AKδL1−δ=Q.
12
设
u=f(x,y,z)
有连续偏导数,
y=y(x)
和
z=z(x)
分别由方程
exy−y=0
和
ex−xz=0
所确定,求
dxdu
.
【答案】
dxdu=∂x∂f+∂y∂f⋅1−xyy2+∂z∂f⋅xz(x−1)
【解析】
由于
u=f(x,y,z)
且
y=y(x)
和
z=z(x)
是由方程
exy−y=0
和
ex−xz=0
所确定的函数,根据链式法则,有:
dxdu=∂x∂f+∂y∂fdxdy+∂z∂fdxdz
需要求
dxdy
和
dxdz
。
对于方程
exy−y=0
,定义
F(x,y)=exy−y
,利用隐函数求导法则:
dxdy=−∂y∂F∂x∂F
计算偏导数:
∂x∂F=yexy,∂y∂F=xexy−1
代入得:
dxdy=−xexy−1yexy=1−xexyyexy
由方程
exy−y=0
得
exy=y
,代入上式:
dxdy=1−xyy⋅y=1−xyy2
对于方程
ex−xz=0
,定义
G(x,z)=ex−xz
,利用隐函数求导法则:
dxdz=−∂z∂G∂x∂G
计算偏导数:
∂x∂G=ex−z,∂z∂G=−x
代入得:
dxdz=−−xex−z=xex−z
由方程
ex−xz=0
得
ex=xz
,代入上式:
dxdz=xxz−z=xz(x−1)
将
dxdy
和
dxdz
代入链式法则公式,即得所求。
13
一商家销售某种商品的价格满足关系
p=7−0.2x
(万元/吨),
x
为销售量(单位:吨),商品的成本函数
C=3x+1
(万元).
(1) 若每销售一吨商品,政府要征税
t
(万元),求该商家获最大利润时的销售量;
(2)
t
为何值时,政府税收总额最大.
【答案】
(1) 销售量
x=10−25t
(2)
t=2
【解析】
(1) 商家的利润函数为
π=(7−0.2x)x−(3x+1)−tx
。简化得
π=−0.2x2+(4−t)x−1.
这是一个二次函数,开口向下,最大值在顶点处。顶点坐标
x=−2ab
,其中
a=−0.2
,
b=4−t
,计算得
x=0.44−t=10−25t.
因此,商家获最大利润时的销售量为
x=10−25t
。
(2) 政府税收总额
T=t×x=t(10−25t)=10t−25t2
。这是一个关于
t
的二次函数,开口向下,最大值在顶点处。顶点坐标
t=−2ab
,其中
a=−25
,
b=10
,计算得
t=510=2.
因此,当
t=2
时,政府税收总额最大。
14
设函数
f(x)
在
[0,+∞)
上连续、单调不减且
f(0)≥0
,试证函数
F(x)={x1∫0xtnf(t)dt,0,若x>0,若x=0,
在
[0,+∞)
上连续且单调不减(其中
n>0
).
【答案】 见解析
【解析】
显然
x>0
时,
F(x)
连续,又由洛必达法则知
x→0+limF(x)=x→0+limx∫0xtnf(t)dt=x→0+limxnf(x)=0=F(0),
所以
F(x)
在
[0,+∞)
上连续。当
x∈(0,+∞)
时,由于
F′(x)=x2xn+1f(x)−∫0xtnf(t)dt=x2∫0xxnf(x)dt−∫0xtnf(t)dt=x2∫0x[xnf(x)−tnf(t)]dt≥0,
可见
F(x)
在
[0,+∞)
上单调不减。
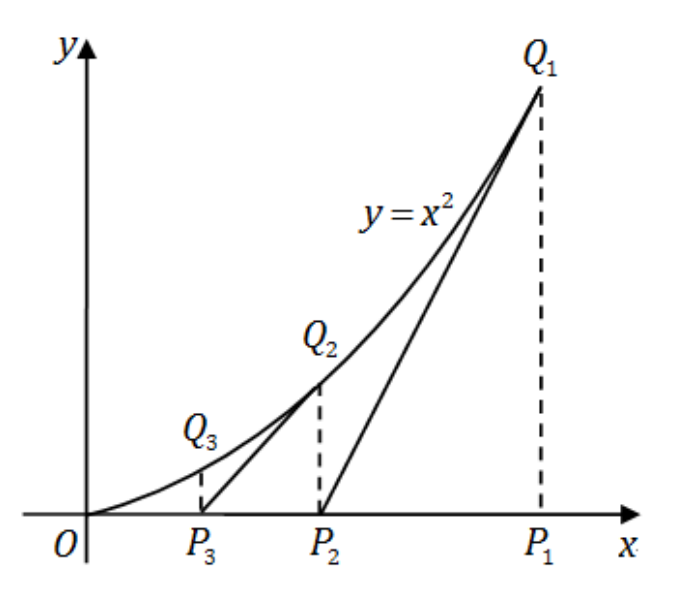
15
从点
P1(1,0)
作
x
轴的垂线,交抛物线
y=x2
于点
Q1(1,1)
;
再从
Q1
作这条抛物线的切线与
x
轴交于
P2
,然后又从
P2
作
x
轴的垂线,交抛物线于点
Q2
,
依次重复上述过程得到一系列的点
P1,Q1;P2,Q2;⋯;Pn,Qn;⋯
.
(1) 求
OPn
;
(2) 求级数
Q1P1+Q2P2+⋯+QnPn+⋯
的和.
其中
n(n≥1)
为自然数,而
M1M2
表示点
M1
与
M2
之间的距离.
【答案】
(1)
OPn=2n−11
(2) 级数
Q1P1+Q2P2+⋯+QnPn+⋯
的和为
34
【解析】
先作草图如下:
由
y=x2
,得
y′=2x
。对于任意
a
(
0<a≤1
),抛物线
y=x2
在点
(a,a2)
处的切线方程为
y−a2=2a(x−a)
。且该切线与
x
轴的交点为
(2a,0)
,故由
OP1=1
可见
OP2=21OP1=21,
OP3=21OP2=21⋅21=221,
⋯
OPn=2n−11.
(II) 由于
QnPn=(OPn)2=(21)2n−2=4n−11⇒n=1∑∞QnPn=n=1∑∞4n−11=m=0∑∞(41)m,
利用几何级数求和公式即得
n=1∑∞QnPn=m=0∑∞(41)m=1−411=34.
16
设函数
f(t)
在
[0,+∞)
上连续,且满足方程
f(t)=e4πt2+∬x2+y2≤4t2f(21x2+y2)dxdy, 求
f(t)
.
【答案】
f(t)=e4πt2(1+4πt2)
【解析】
给定函数
f(t)
在
[0,+∞)
上连续,且满足方程:
f(t)=e4πt2+∬x2+y2≤4t2f(21x2+y2)dxdy 首先,将积分转换为极坐标。令
x=rcosθ
,
y=rsinθ
,则
dxdy=rdrdθ
,积分区域为
r≤2t
,
θ∈[0,2π]
。被积函数为
f(2r)
,因此:
∬x2+y2≤4t2f(21x2+y2)dxdy=∫02π∫02tf(2r)rdrdθ=2π∫02tf(2r)rdr 令
u=2r
,则
r=2u
,
dr=2du
,积分限变为
u∈[0,t]
:
2π∫02tf(2r)rdr=2π∫0tf(u)⋅2u⋅2du=8π∫0tf(u)udu
原方程化为:
f(t)=e4πt2+8π∫0tf(u)udu
令
F(t)=∫0tf(u)udu
,则
F′(t)=f(t)t
。对原方程两边求导:
f′(t)=dtde4πt2+8πF′(t)=8πte4πt2+8πtf(t)
整理得一阶线性微分方程:
f′(t)−8πtf(t)=8πte4πt2
积分因子为
μ(t)=e∫−8πtdt=e−4πt2
。两边乘以积分因子:
e−4πt2f′(t)−8πte−4πt2f(t)=8πt
左边为
dtd(f(t)e−4πt2)
,故:
dtd(f(t)e−4πt2)=8πt
积分得:
f(t)e−4πt2=∫8πtdt=4πt2+C
即:
f(t)=e4πt2(4πt2+C)
由初始条件
f(0)=1
,代入得:
f(0)=e0(0+C)=C=1
所以
C=1
,因此:
f(t)=e4πt2(1+4πt2)
验证可知满足原方程。
17
设
A
为
n
阶非奇异矩阵,
α
为
n
维列向量,
b
为常数.记分块矩阵
P=(E−αTA∗0∣A∣),Q=(AαTαb),
其中
A∗
是矩阵
A
的伴随矩阵,
E
为
n
阶单位矩阵.
(1) 计算并化简
PQ
;
(2) 证明:矩阵
Q
可逆的充分必要条件是
αTA−1α=b
.
【答案】
(1)
PQ=(A0α∣A∣(b−αTA−1α))
(2) 矩阵
Q
可逆的充分必要条件是
αTA−1α=b
。
【解析】
(1) 计算
PQ
:
设
P=(E−αTA∗0∣A∣),Q=(AαTαb).
则
PQ=(E⋅A+0⋅αT(−αTA∗)A+∣A∣αTE⋅α+0⋅b(−αTA∗)α+∣A∣b)=(A−αTA∗A+∣A∣αTα−αTA∗α+∣A∣b).
由于
A
非奇异,有
A∗A=∣A∣E
,代入得
−αTA∗A+∣A∣αT=−αT∣A∣E+∣A∣αT=−∣A∣αT+∣A∣αT=0.
又
A∗=∣A∣A−1
,所以
−αTA∗α+∣A∣b=−αT∣A∣A−1α+∣A∣b=∣A∣(−αTA−1α+b)=∣A∣(b−αTA−1α).
因此,
PQ=(A0α∣A∣(b−αTA−1α)).
(2) 证明
Q
可逆的充分必要条件是
αTA−1α=b
:
首先,
P
可逆,因为
P
是分块下三角矩阵,其行列式
∣P∣=∣E∣⋅∣A∣=∣A∣=0
。由于
P
可逆,
Q
可逆当且仅当
PQ
可逆。
由 (1) 知
PQ=(A0αd),d=∣A∣(b−αTA−1α).
PQ
是分块上三角矩阵,其行列式
∣PQ∣=∣A∣⋅d=∣A∣⋅∣A∣(b−αTA−1α)=∣A∣2(b−αTA−1α).
由于
∣A∣=0
,
∣PQ∣=0
当且仅当
b−αTA−1α=0
,即
αTA−1α=b
。
因此,
Q
可逆当且仅当
αTA−1α=b
。
18
设三阶实对称矩阵
A
的特征值是
1
,
2
,
3
;矩阵
A
的属于特征值
1
,
2
的特征向量分别是
α1=(−1,−1,1)T,α2=(1,−2,−1)T
.
(1) 求
A
的属于特征值
3
的特征向量;
(2) 求矩阵
A
.
【答案】
(1)
A
的属于特征值
3
的特征向量为
(1,0,1)T
。
(2) 矩阵
A
为
613−3165−3135316531613
。
【解析】
(1) 由于
A
是实对称矩阵,属于不同特征值的特征向量相互正交。设属于特征值
3
的特征向量为
α3=(x,y,z)T
,则
α3
与
α1=(−1,−1,1)T
和
α2=(1,−2,−1)T
正交,即
α3⋅α1=−x−y+z=0,α3⋅α2=x−2y−z=0.
解方程组得
y=0
,
z=x
,因此
α3=(1,0,1)T
(取非零标量倍)。
(2) 已知特征值
λ1=1
,
λ2=2
,
λ3=3
对应的单位特征向量为
u1=∥α1∥α1=(−31,−31,31)T u2=∥α2∥α2=(61,−62,−61)T u3=∥α3∥α3=(21,0,21)T 利用谱分解
A=λ1u1u1T+λ2u2u2T+λ3u3u3T
,计算外积
u1u1T=3131−313131−31−31−3131,u2u2T=61−31−61−313231−613161,u3u3T=2102100021021. 乘以特征值后求和
A=1⋅u1u1T+2⋅u2u2T+3⋅u3u3T=613−3165−3135316531613. 验证:
Aα1=α1
,
Aα2=2α2
,
Aα3=3α3
,符合要求。
19
假设随机变量
X
的绝对值不大于
1
;
P{X=−1}=81,P{X=1}=41
;
在事件
{−1<X<1}
出现的条件下,
X
在
(−1,1)
内的任一子区间上取值的条件概率与该子区间长度成正比.
试求
X
的分布函数
F(x)=P{X≤x}
.
【答案】
F(x)=⎩⎨⎧0165x+71 x<−1 −1≤x<1 x≥1 【解析】
由
X
的绝对值不大于 1,可得:当
x<−1
时,
F(x)=P{X≤x}=0
;当
x≥1
时,
F(x)=P{X≤x}=1
。又
P{X=−1}=81
,
P{X=1}=41
,则
P{−1<x<1}=1−P{X=−1}−P{X=1}=1−81−41=85
由题意
X
在
(−1,1)
内的任一子区间上取值的条件概率与该子区间长度成正比,那么当
X
的值属于
(−1,1)
的条件下,事件
{−1<X≤x}
的条件概率为:
P{−1<X≤x∣−1<X<1}=k1−(−1)x−(−1)=k2x+1,
其中
k
为比例正常数。又
P{−1<X<1∣−1<X<1}=1
,而
P{−1<X<1∣−1<X<1}=k21+1=k
所以
k=1
,故
P{−1<X≤x∣−1<X<1}=2x+1
当
−1<x<1
时,
{−1<X≤x}={−1<X≤x}∩{−1<X<1}
所以
P{−1<X≤x}=P{−1<X≤x,−1<X<1}
由条件概率公式,有
P{−1<X≤x}=P{−1<X≤x,−1<X<1}=P{−1<X≤x∣−1<X<1}P{−1<X<1}=2x+1×85=165x+5,
F(x)=P{X≤x}=P{X≤−1}+P{−1<X≤x},而
P{X≤−1}=P{X=−1}+P{X<−1}=81+0=81
所以
F(x)=P{X≤x}=P{X≤−1}+P{−1<X≤x}=81+165x+5=165x+7,
故所求的
X
的分布函数为
F(x)=⎩⎨⎧0,165x+7,1,x<−1;−1≤x<1;x≥1. 20
游客乘电梯从底层到电视塔顶层观光;电梯于每个整点的第
5
分钟、
25
分钟和
55
分钟从底层起行.
假设一游客在早晨八点的第
X
分钟到达底层候梯处,且
X
在
[0,60]
上均匀分布,求该游客等候时间的数学期望.
【答案】
335
【解析】
已知
X
在
[0,60]
上均匀分布,则其密度函数为:
f(x)={601,0,0≤x≤60,其他.
设
Y
表示游客等候电梯的时间(单位:分钟),则
Y=g(X)=⎩⎨⎧5−X,25−X,55−X,65−X,0≤X≤5,5<X≤25,25<X≤55,55<X≤60. 由随机变量函数期望的定义,有
EY=∫−∞+∞g(x)f(x)dx=601∫060g(x)dx=601[∫05(5−x)dx+∫525(25−x)dx+∫2555(55−x)dx+∫5560(65−x)dx]=601(12.5+200+450+37.5)=11.67.
21
两台同样自动记录仪,每台无故障工作的时间服从参数为
5
的指数分布;
首先开动其中一台,当其发生故障时停用而另一台自行开动.
试求两台记录仪无故障工作的总时间
T
的概率密度
f(t)
、数学期望和方差.
【答案】
概率密度函数:
f(t)=25te−5t,t≥0
数学期望:
E[T]=52
方差:
Var(T)=252
【解析】
设
X1
和
X2
表示先后开动的记录仪无故障工作的时间,则两台记录仪无故障工作的总时间为
T=X1+X2
。由于每台无故障工作的时间都服从参数为 5 的指数分布,则
X1
和
X2
的概率密度函数为
f(x)={5e−5x,0,x>0;x≤0.
因为两台仪器是独立的,则其无故障工作的时间显然也是相互独立的,即
X1
和
X2
独立,由卷积公式:当
t>0
时,
T
的概率密度为
f(t)=∫−∞+∞f1(x)f2(t−x)dx=25∫0te−5xe−5(t−x)dx=25te−5t;
当
t≤0
时,
f(t)=0
,即
f(t)={25te−5t,0,t>0;t≤0.
由指数分布的期望和方差的结论,有
EX1=EX2=λ1=51,DX1=DX2=λ21=251.
由期望的性质有
ET=E(X1+X2)=EX1+EX2=51+51=52.
由独立随机变量方差的性质有
DT=D(X1+X2)=DX1+DX2=251+251=252.