2008 年真题

选择题

1

设 $x=0$ 是函数 $g(x)=\frac{\int_{0}^{x} f(t) dt}{x}$ 的()

正确答案：B

详解

对于极限表达式：

\lim _{x \to 0} g(x) = \lim _{x \to 0} \frac{\int_{0}^{x} f(t) d t}{x}

应用洛必达法则，得到：

\lim _{x \to 0} \frac{\int_{0}^{x} f(t) d t}{x} = \lim _{x \to 0} f(x) = f(0)

因此， $x=0$ 是函数 $g(x)$ 的可去间断点。

2

曲线段方程为 $y = f(x)$ ，函数 $f(x)$ 在区间 $[0, a]$ 上有连续的导数，则定积分

\int_{0}^{a} x f'(x) \, dx

等于()

高等数学一元函数积分学定积分的应用

正确答案：C

详解

首先，我们来看积分 $\int_{0}^{a} x f'(x) d x$ 的计算过程：

\int_{0}^{a} x f'(x) d x = \int_{0}^{a} x d f(x) = \left. x f(x) \right|_{0}^{a} - \int_{0}^{a} f(x) d x = a f(a) - \int_{0}^{a} f(x) d x

接下来，我们从几何角度解释这个结果：

$a f(a)$ 表示矩形 ABOC 的面积。
$\int_{0}^{a} f(x) d x$ 表示曲边梯形 ABO 的面积。

因此， $\int_{0}^{a} x f'(x) d x$ 实际上表示的是曲边三角形的面积。

3

已知 $f(x, y) = e^{\sqrt{x^{2} + y^{2}}}$ ，则()

高等数学多元函数微分学偏导数的概念与计算

正确答案：B

详解

计算 $f_x'(0,0)$ ：

f_{x}'(0,0) = \lim _{x \to 0} \frac{f(x, 0)-f(0,0)}{x-0} = \lim _{x \to 0} \frac{e^{\sqrt{x^{2}+0^{2}}}-1}{x} = \lim _{x \to 0} \frac{e^{|x|}-1}{x}

分别计算左右极限：

\lim _{x \to 0^{+}} \frac{e^{x}-1}{x} = 1, \quad \lim _{x \to 0^{-}} \frac{e^{-x}-1}{x} = -1

由于左右极限不相等，故 $f_x'(0,0)$ 不存在。

计算 $f_y'(0,0)$ ：

f_{y}'(0,0) = \lim _{y \to 0} \frac{f(0, y)-f(0,0)}{y-0} = \lim _{y \to 0} \frac{e^{\sqrt{0+y^{2}}}-1}{y} = \lim _{y \to 0} \frac{e^{|y|}-1}{y}

当 $y \to 0$ 时， $|y| \to 0$ ，且 $e^{|y|}-1 \sim |y|$ 。因此：

\lim _{y \to 0} \frac{e^{|y|}-1}{y} = 0

所以 $f_y'(0,0)$ 存在。综上，正确答案为 B。

4

设 $F(u, v) = \iint_{D_{uv}} \frac{f(x^{2} + y^{2})}{\sqrt{x^{2} + y^{2}}} \, dx \, dy$ ，其中 $D_{uv}$ 为圆环域 $1 \leq x^{2} + y^{2} \leq u^{2}$ ， $0 \leq v \leq 2\pi$ ，则 $\frac{\partial F}{\partial u} = (\ )$ 。

高等数学多元函数积分学重积分的计算

正确答案：A

详解

使用极坐标变换得到：

F(u, v) = \iint_{D} \frac{f\left(r^{2}\right)}{r} \cdot r \, dr \, d\theta = \int_{0}^{v} d\theta \int_{1}^{u} f\left(r^{2}\right) \, dr = v \int_{1}^{u} f\left(r^{2}\right) \, dr

因此：

\frac{\partial F}{\partial u} = v f\left(u^{2}\right)

5

设 $A$ 为 $n$ 阶非零矩阵， $E$ 为 $n$ 阶单位矩阵，若 $A^{3} = \boldsymbol{0}$ ，则()

线性代数矩阵伴随矩阵与可逆矩阵

正确答案：C

详解

我们有：

(E - A)(E + A + A^{2}) = E - A^{3} = E

以及：

(E + A)(E - A + A^{2}) = E + A^{3} = E

因此， $E - A$ 和 $E + A$ 均可逆。

6

设 $\boldsymbol{A} = \begin{pmatrix}1 & 2 \\ 2 & 1\end{pmatrix}$ ，则与 $\boldsymbol{A}$ 合同的矩阵为()

线性代数二次型

正确答案：D

详解

记矩阵 $D = \begin{pmatrix}1 & -2 \\ -2 & 1\end{pmatrix}$ ，则其特征多项式为：

|\lambda E - D| = \begin{vmatrix}\lambda - 1 & 2 \\ 2 & \lambda - 1\end{vmatrix} = (\lambda - 1)^{2} - 4

对于矩阵 $A$ ，其特征多项式为：

|\lambda E - A| = \begin{vmatrix}\lambda - 1 & -2 \\ -2 & \lambda - 1\end{vmatrix} = (\lambda - 1)^{2} - 4

因此， $A$ 和 $D$ 具有相同的特征多项式，即相同的特征值。

由于 $A$ 和 $D$ 是同阶实对称矩阵，而实对称矩阵相似必合同，故选项 D 正确。

7

随机变量 $X$ 、 $Y$ 独立同分布且 $X$ 的分布函数为 $F(x)$ ，则 $Z = \max\{X, Y\}$ 的分布函数为

概率论与数理统计多维随机变量及其分布二维随机变量及其分布

正确答案：A

详解

设 $Z = \max\{X, Y\}$ ，则其分布函数为：

F_Z(z) = P(Z \leq z) = P\{\max\{X, Y\} \leq z\}

由于 $\max\{X, Y\} \leq z$ 等价于 $X \leq z$ 且 $Y \leq z$ ，且 $X$ 和 $Y$ 独立，因此：

F_Z(z) = P(X \leq z)P(Y \leq z) = F(z)F(z) = F^{2}(z)

其中 $F(z)$ 为 $X$ 和 $Y$ 的公共分布函数。

8

随机变量 $X \sim N(0,1)$ ， $Y \sim N(1,4)$ 且相关系数 $\rho_{XY} = 1$ ，则 ( )

概率论与数理统计随机变量的数字特征协方差与相关系数

正确答案：D

详解

设 $Y = aX + b$ 。由 $\rho_{XY} = 1$ 可知 $X$ 和 $Y$ 正相关，因此 $a > 0$ ，排除选项 (A) 和 (C)。

已知 $X \sim N(0,1)$ 和 $Y \sim N(1,4)$ ，则：

E(X) = 0, \quad E(Y) = 1

根据线性变换的期望：

E(Y) = E(aX + b) = aE(X) + b = b = 1

因此 $b = 1$ ，排除选项 (B)。最终选择 (D)。

填空题

9

（填空题）设函数

f(x)= \begin{cases} x^{2}+1, & |x| \leq c \\ \frac{2}{|x|}, & |x| > c \end{cases}

在 $(-\infty,+\infty)$ 内连续，则 $c=$ ________

高等数学函数、极限、连续函数的连续性

【答案】 1

【解析】 因为 $\lim _{x \to c^{-}} f(x) = \lim _{x \to c^{-}} \left(x^{2} + 1\right) = c^{2} + 1$ ，而 $\lim _{x \to c^{+}} f(x) = \lim _{x \to c^{+}} \frac{2}{|x|} = \frac{2}{c}$ 。

由于 $f(x)$ 在 $(-\infty, +\infty)$ 内连续，必然在 $x = c$ 处连续，因此有：

\lim _{x \to c^{+}} f(x) = \lim _{x \to c^{-}} f(x) = f(c)

即：

c^{2} + 1 = \frac{2}{c}

解得 $c = 1$ 。

10

（填空题）设 $f\left(x + \frac{1}{x}\right) = \frac{x + x^{3}}{1 + x^{4}}$ ，则 $\int_{2}^{2\sqrt{2}} f(x) \, dx =$

高等数学一元函数积分学定积分的计算

【答案】 $\frac{1}{2} \ln 3$

【解析】 给定函数关系式：

f\left(x+\frac{1}{x}\right) = \frac{\frac{1}{x} + x}{\frac{1}{x^{2}} + x^{2}} = \frac{\frac{1}{x} + x}{\left(\frac{1}{x} + x\right)^{2} - 2}

令 $t = \frac{1}{x} + x$ ，则函数可表示为：

f(t) = \frac{t}{t^{2} - 2}

于是，积分计算如下：

\int_{2}^{2\sqrt{2}} f(x) \, dx = \int_{2}^{2\sqrt{2}} \frac{x}{x^{2} - 2} \, dx

利用换元积分法，得到：

\frac{1}{2} \ln \left(x^{2} - 2\right) \bigg|_{2}^{2\sqrt{2}} = \frac{1}{2} \left(\ln 6 - \ln 2\right) = \frac{1}{2} \ln 3

最终结果为：

\frac{1}{2} \ln 3

11

（填空题）设 $D = \{(x, y) \mid x^{2} + y^{2} \leq 1\}$ ，则

\iint_{D} \left(x^{2} - y\right) \, dx \, dy = \underline{\quad}

高等数学多元函数积分学重积分的计算

【答案】 $\frac{\pi}{8}$

【解析】 利用函数奇偶性，区域 $D$ 关于 $x$ 轴对称， $y$ 是关于 $y$ 的奇函数，所以

\iint_{D} (-y) \, dx dy = 0

对于 $\iint_{D} x^{2} \, dx dy$ ，利用极坐标计算：

\int_{0}^{2\pi} d\theta \int_{0}^{1} r^{2} \cos^{2}\theta \cdot r \, dr = \int_{0}^{2\pi} \cos^{2}\theta \, d\theta \int_{0}^{1} r^{3} \, dr = \frac{\pi}{2} \times \frac{1}{4} = \frac{\pi}{8}

因此，

\iint_{D} \left(x^{2} - y\right) dx dy = \frac{\pi}{8}

12

（填空题）微分方程 $x y' + y = 0$ 满足条件 $y(1) = 1$ 的解为 $y =$

高等数学常微分方程可分离变量的微分方程与齐次方程

【答案】 $y = \frac{1}{x}$

【解析】 方程可化为

\frac{d y}{d x} = -\frac{y}{x}

分离变量得

-\ln |y| = \ln |x| + C_{1}

即

\frac{1}{|y|} = |x| \cdot C

又 $y(1) = 1$ ，所以 $C = 1$ ，故

y = \frac{1}{x}

13

（填空题）设3阶矩阵 $A$ 的特征值为1，2，2， $E$ 为3阶单位矩阵，则 $\left|4 A^{-1} - E\right| =$ ____________

线性代数矩阵的特征值与特征向量

【答案】 3

【解析】 $A$ 的特征值为1，2，2，所以 $A^{-1}$ 的特征值为1， $\frac{1}{2}$ ， $\frac{1}{2}$ 。

则 $4 A^{-1} - E$ 的特征值为：

4 \times 1 - 1 = 3

4 \times \frac{1}{2} - 1 = 1

4 \times \frac{1}{2} - 1 = 1

所以行列式的值为：

|4 A^{-1} - E| = 3 \times 1 \times 1 = 3

14

（填空题）设随机变量 $X$ 服从参数为 1 的泊松分布，则 $P\{X = E(X^{2})\} =$

概率论与数理统计随机变量及其分布

【答案】 $\frac{1}{2} e^{-1}$

【解析】 由 $D X=E X^{2}-(E X)^{2}$ ， $X$ 服从参数为1的泊松分布，故 $E X=D X=1$ 。

因此， $E X^{2}=1 + 1^{2}=2$ 。

于是，

P\{X=2\}=\frac{1^{2}}{2!} e^{-1}=\frac{1}{2} e^{-1}

解答题

15

（本题满分 10 分）

求极限

\lim _{x \to 0} \frac{1}{x^{2}} \ln \left( \frac{\sin x}{x} \right)

高等数学函数、极限、连续函数极限的计算

【答案】 -1/6

【解析】
方法一：

\begin{align*} \lim _{x \to 0} \frac{1}{x^{2}} \ln \frac{\sin x}{x} &= \lim _{x \to 0} \frac{1}{x^{2}} \ln \left(1 + \frac{\sin x}{x} - 1\right) \\ &= \lim _{x \to 0} \frac{\sin x - x}{x^{3}} \\ &= \lim _{x \to 0} \frac{\cos x - 1}{3 x^{2}} \\ &= -\lim _{x \to 0} \frac{\sin x}{6 x} \\ &= -\frac{1}{6} \end{align*}

洛必达法则：

\lim _{x \to 0} \frac{-x \sin x}{6 x^{2}} = -\frac{1}{6}

16

（本题满分 10 分）

设 $z = z(x, y)$ 是由方程 $x^{2} + y^{2} - z = \varphi(x + y + z)$ 所确定的函数，其中 $\varphi$ 具有 2 阶导数且 $\varphi' \neq -1$ 时。

(1) 求 $dz$

(2) 记 $u(x, y) = \frac{1}{x - y}\left(\frac{\partial z}{\partial x} - \frac{\partial z}{\partial y}\right)$ ，求 $\frac{\partial u}{\partial x}$

多元函数微分学全微分的概念与计算

【答案】
(1) $dz = \frac{(-\varphi' + 2x)dx + (-\varphi' + 2y)dy}{\varphi' + 1}$
(2) $\frac{\partial u}{\partial x} = -\frac{4x\varphi''}{(\varphi' + 1)^{3}}$

【解析】
(1)

2x dx + 2y dy - dz = \varphi'(x + y + z) \cdot (dx + dy + dz)

(\varphi' + 1)dz = (-\varphi' + 2x)dx + (-\varphi' + 2y)dy

dz = \frac{(-\varphi' + 2x)dx + (-\varphi' + 2y)dy}{\varphi' + 1} \quad (\because \varphi' \neq -1)

(2)

由上一问可知：

\frac{\partial z}{\partial x} = \frac{-\varphi' + 2x}{\varphi' + 1}, \quad \frac{\partial z}{\partial y} = \frac{-\varphi' + 2y}{\varphi' + 1}

所以：

u(x, y) = \frac{1}{x - y}\left(\frac{\partial z}{\partial x} - \frac{\partial z}{\partial y}\right) = \frac{1}{x - y}\left(\frac{-\varphi' + 2x}{\varphi' + 1} - \frac{-\varphi' + 2y}{\varphi' + 1}\right)

= \frac{1}{x - y} \frac{-2y + 2x}{\varphi' + 1} = \frac{2}{\varphi' + 1}

所以：

\frac{\partial u}{\partial x} = \frac{-2\varphi''\left(1 + \frac{\partial z}{\partial x}\right)}{(\varphi' + 1)^{2}} = -\frac{2\varphi''\left(1 + \frac{2x - \varphi'}{1 + \varphi'}\right)}{(\varphi' + 1)^{2}}

= -\frac{2\varphi''(1 + \varphi' + 2x - \varphi')}{(\varphi' + 1)^{3}} = -\frac{2(2x)\varphi''}{(\varphi' + 1)^{3}}

17

（本题满分11分）

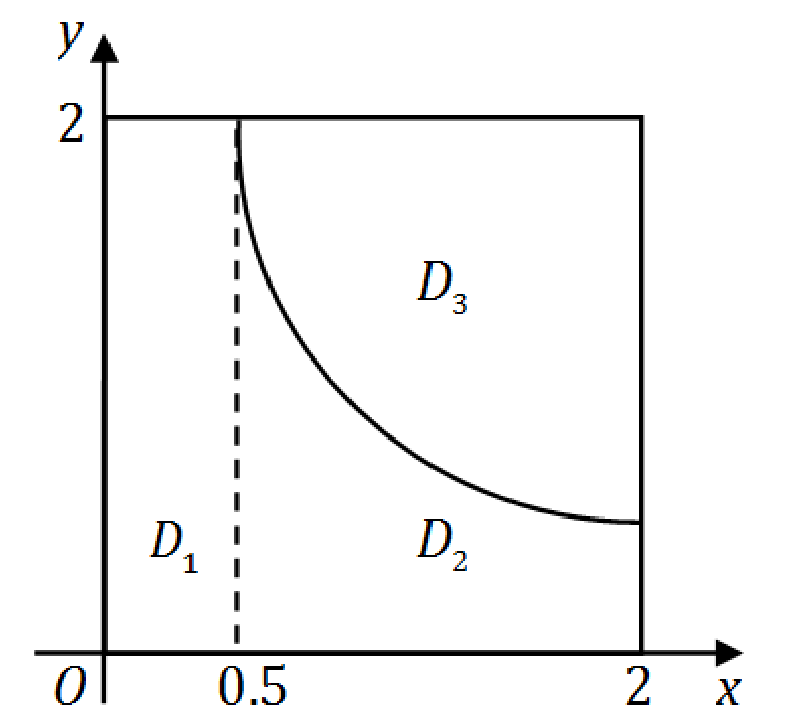
计算 $\iint_{D} \max(xy, 1) \, dx \, dy$ ，其中 $D = \{(x, y) \mid 0 \leq x \leq 2, 0 \leq y \leq 2\}$ 。

高等数学多元函数积分学重积分的计算

【答案】 $\frac{19}{4} + \ln 2$

【解析 曲线 $xy = 1$ 将区域分成两个区域 $D_{1}$ 和 $D_{2} + D_{3}$ 。为了便于计算，继续对区域进行分割，最终结果为：

\begin{aligned} & \iint_{D} \max(xy, 1) dx dy \\ & = \iint_{D_{1}} xy dx dy + \iint_{D_{2}} 1 dx dy + \iint_{D_{3}} 1 dx dy \\ & = \int_{0}^{1} dx \int_{0}^{\frac{1}{x}} xy dy + \int_{0}^{1} dx \int_{\frac{1}{x}}^{2} 1 dy + \int_{1}^{2} dx \int_{0}^{2} 1 dy \\ & = \int_{0}^{1} \left[\frac{1}{2}xy^{2}\right]_{0}^{\frac{1}{x}} dx + \int_{0}^{1} \left(2 - \frac{1}{x}\right) dx + \int_{1}^{2} 2 dx \\ & = \int_{0}^{1} \frac{1}{2x} dx + \left[2x - \ln x\right]_{0}^{1} + 2 \\ & = \frac{1}{2} \ln x \big|_{0}^{1} + (2 - 0) + 2 \quad \text{} \\ & = \int_{0}^{1} dx \int_{0}^{\frac{1}{x}} xy dy + \int_{\frac{1}{2}}^{2} dx \int_{\frac{1}{x}}^{2} xy dy + \int_{0}^{\frac{1}{2}} dx \int_{0}^{2} 1 dy + \int_{\frac{1}{2}}^{2} dx \int_{0}^{\frac{1}{x}} 1 dy \\ & = \int_{0}^{1} \frac{1}{2x} dx + \int_{\frac{1}{2}}^{2} \left(\frac{1}{2}x \cdot 4 - \frac{1}{2x}\right) dx + \left[x\right]_{0}^{\frac{1}{2}} \cdot 2 + \int_{\frac{1}{2}}^{2} \frac{1}{x} dx \\ & = \frac{1}{2} \ln 1 - \frac{1}{2} \ln 0^+ + \int_{\frac{1}{2}}^{2} \left(2x - \frac{1}{2x}\right) dx + 1 + \ln 2 - \ln \frac{1}{2} \\ & = 1 + 2 \ln 2 + \frac{15}{4} - \ln 2 \\ & = \frac{19}{4} + \ln 2 \end{aligned}

18

（本题满分10分）

设 $f(x)$ 是周期为2的连续函数。

(1) 证明对任意实数 $t$ ，有

\int_{t}^{t+2} f(x) \, dx = \int_{0}^{2} f(x) \, dx

(2) 证明

G(x) = \int_{0}^{x} \left[ 2f(t) - \int_{t}^{t+2} f(s) \, ds \right] dt

是周期为2的周期函数。

高等数学一元函数积分学定积分的计算

【答案】 见解析

【解析】 (1) 由积分的性质知对任意的实数 $t$ ，

\int_{t}^{t+2} f(x) dx = \int_{t}^{0} f(x) dx + \int_{0}^{2} f(x) dx + \int_{2}^{t+2} f(x) dx

令 $x = 2 + u$ ，则

\int_{2}^{t+2} f(x) dx = \int_{0}^{t} f(2 + u) du = \int_{0}^{t} f(u) du = -\int_{t}^{0} f(x) dx

因此，

\int_{t}^{t+2} f(x) dx = \int_{t}^{0} f(x) dx + \int_{0}^{2} f(x) dx - \int_{t}^{0} f(x) dx = \int_{0}^{2} f(x) dx

另一种方法：设 $F(t) = \int_{t}^{t+2} f(x) dx$ 。由于

F'(t) = f(t+2) - f(t) = 0

所以 $F(t)$ 为常数，从而有 $F(t) = F(0)$ 。而

F(0) = \int_{0}^{2} f(x) dx

因此，

\int_{t}^{t+2} f(x) dx = \int_{0}^{2} f(x) dx

(2) 由(1)知，对任意的 $t$ 有

\int_{t}^{t+2} f(s) ds = \int_{0}^{2} f(s) ds

记 $a = \int_{0}^{2} f(s) ds$ ，则

G(x) = 2 \int_{0}^{x} f(t) dt - a x

对任意的 $x$ ，

\begin{aligned} G(x+2) - G(x) & = 2 \int_{0}^{x+2} f(t) dt - a(x+2) - 2 \int_{0}^{x} f(t) dt + a x \\ & = 2 \int_{x}^{x+2} f(t) dt - 2a \\ & = 2 \int_{0}^{2} f(t) dt - 2a = 0 \end{aligned}

所以 $G(x)$ 是周期为2的周期函数。

19

（本题满分 10 分）

设银行存款的年利率为 $r = 0.05$ ，并依年复利计算。某基金会希望通过存款 $A$ 万元，实现：

第一年提取 $19$ 万元，
第二年提取 $28$ 万元，
$\cdots$ ，
第 $n$ 年提取 $(10 + 9n)$ 万元，

并能按此规律一直提取下去。问 $A$ 至少应为多少万元？

高等数学无穷级数幂级数的和函数及幂级数展开式

【答案】 3980 万元

【解析】 方法一：设 $A_{n}$ 为用于第 $n$ 年提取 $(10 + 9n)$ 万元的贴现值，则

A_{n} = (1 + r)^{-n}(10 + 9n)

因此，总现值为：

A = \sum_{n=1}^{\infty} A_{n} = \sum_{n=1}^{\infty} \frac{10 + 9n}{(1 + r)^{n}} = 10 \sum_{n=1}^{\infty} \frac{1}{(1.05)^{n}} + 9 \sum_{n=1}^{\infty} \frac{n}{(1.05)^{n}}

设 $S(x) = \sum_{n=1}^{\infty} n x^{n}$ （ $|x| < 1$ ），因为：

S(x) = x \sum_{n=1}^{\infty} n x^{n-1} = x \cdot \frac{1}{(1 - x)^{2}} = \frac{x}{(1 - x)^{2}}

所以：

S\left(\frac{1}{1.05}\right) = \frac{\frac{1}{1.05}}{\left(1 - \frac{1}{1.05}\right)^{2}} = 420 \quad \text{}

最终结果为：

A = 10 \times \frac{\frac{1}{1.05}}{1 - \frac{1}{1.05}} + 9 \times 420 = 10 \times 20 + 3780 = 3980 \quad \text{}

方法二：设第 $t$ 年取款后的余款为 $y_{t}$ ，由题意知 $y_{t}$ 满足方程：

y_{t} = (1 + 0.05)y_{t-1} - (10 + 9t)

即：

y_{t} - 1.05y_{t-1} = -(10 + 9t)

对应的齐次方程通解为：

y_{t} = C(1.05)^{t}

设特解为 $y_{t} = at + b$ ，代入解得：

a = 180, \quad b = 3980

所以通解为：

y_{t} = C(1.05)^{t} + 180t + 3980

由初始条件 $y_{0} = A$ 及 $y_{t} \geq 0$ 得：

A = C + 3980 \quad \text{} \quad C \geq 0

因此， $A$ 至少为 3980 万元。

20

（本题满分 12 分）

设

\boldsymbol{A} = \begin{pmatrix} 2a & 1 & & & \\ a^{2} & 2a & 1 & & \\ & a^{2} & 2a & \ddots & \\ & & \ddots & \ddots & 1 \\ & & & a^{2} & 2a \end{pmatrix}_{n \times n}, \quad \boldsymbol{X} = \begin{pmatrix} x_{1} \\ \vdots \\ x_{n} \end{pmatrix}, \quad \boldsymbol{B} = \begin{pmatrix} 1 \\ 0 \\ \vdots \\ 0 \end{pmatrix}

求证 $|\boldsymbol{A}| = (n + 1)a^{n}$
$a$ 为何值时，方程组 $\boldsymbol{AX} = \boldsymbol{B}$ 有唯一解；
$a$ 为何值时，方程组 $\boldsymbol{AX} = \boldsymbol{B}$ 有无穷多解。

线性代数矩阵伴随矩阵与可逆矩阵

【答案】

见解析
$a \neq 0$
$a = 0$

【解析】
(1) 证法一：通过行列式行变换（如 $r_{i+1} - \frac{i}{i+1}a r_{i}$ ）将矩阵化为上三角，得行列式为

2a \cdot \frac{3a}{2} \cdot \frac{4a}{3} \cdots \frac{(n+1)a}{n} = (n+1)a^{n}

证法二：数学归纳法。当 $n=1$ 时， $|A|=2a$ ；假设 $n=k$ 时成立，即 $D_{k}=(k+1)a^{k}$ ，则 $n=k+1$ 时，按第一行展开得

D_{k+1}=2aD_{k} - a^{2}D_{k-1}=2a(k+1)a^{k} - a^{2}k a^{k-1}=(k+2)a^{k+1}

结论成立。

证法三：递推法。记 $D_{n}=|A|$ ，则 $D_{n}=2aD_{n-1} - a^{2}D_{n-2}$ ，特征方程 $r^{2}-2ar + a^{2}=0$ 得重根 $r=a$ ，通解

D_{n}=(C_{1}+C_{2}n)a^{n}

代入初始条件 $D_{1}=2a$ ， $D_{2}=3a^{2}$ 得 $C_{1}=1$ ， $C_{2}=1$ ，故

D_{n}=(n+1)a^{n}

(2) 方程组有唯一解当且仅当 $|A| \neq 0$ ，即 $(n+1)a^{n} \neq 0$ ，故 $a \neq 0$ 。

(3) 方程组有无穷多解当且仅当 $|A|=0$ 且系数矩阵与增广矩阵秩相等。由 $|A|=0$ 得 $a=0$ ，此时矩阵 $A$ 为零矩阵（除第一行第一列为0，其余位置？需结合原矩阵结构，实际当 $a=0$ 时， $A$ 为上三角矩阵，主对角线为0，第一行为 $(0,1,0,\cdots,0)$ ，其余行前两列依次为 $0,0$ 等，增广矩阵为 $(1,0,\cdots,0)^{\top}$ ，此时系数矩阵秩为 $n-1$ ，增广矩阵秩也为 $n-1$ ，故 $a=0$ 时有无穷多解。

21

（本题满分 10 分）

设 $A$ 为 3 阶矩阵， $\boldsymbol{a}_{1}$ 、 $\boldsymbol{a}_{2}$ 为 $A$ 的分别属于特征值 $-1$ 、 $1$ 的特征向量，向量 $\boldsymbol{a}_{3}$ 满足 $A\boldsymbol{a}_{3} = \boldsymbol{a}_{2} + \boldsymbol{a}_{3}$ 。证明：

$\boldsymbol{a}_{1}$ 、 $\boldsymbol{a}_{2}$ 、 $\boldsymbol{a}_{3}$ 线性无关；
令 $P = (\boldsymbol{a}_{1}, \boldsymbol{a}_{2}, \boldsymbol{a}_{3})$ ，求 $P^{-1}AP$ 。

线性代数矩阵的特征值与特征向量

【答案】

见解析
$\begin{pmatrix} -1 & 0 & 0 \\ 0 & 1 & 1 \\ 0 & 0 & 1 \end{pmatrix}$

【解析】
(1)

证法一：假设 $\boldsymbol{\alpha}_{1}$ , $\boldsymbol{\alpha}_{2}$ , $\boldsymbol{\alpha}_{3}$ 线性相关。因为 $\boldsymbol{\alpha}_{1}$ , $\boldsymbol{\alpha}_{2}$ 分别属于不同特征值的特征向量，故 $\boldsymbol{\alpha}_{1}$ , $\boldsymbol{\alpha}_{2}$ 线性无关。则 $\boldsymbol{\alpha}_{3}$ 可由 $\boldsymbol{\alpha}_{1}$ , $\boldsymbol{\alpha}_{2}$ 线性表出，不妨设 $\boldsymbol{\alpha}_{3} = l_{1} \boldsymbol{\alpha}_{1} + l_{2} \boldsymbol{\alpha}_{2}$ ，其中 $l_{1}, l_{2}$ 不全为零（若 $l_{1}, l_{2}$ 同时为 0，则 $\boldsymbol{\alpha}_{3} = 0$ ，由 $A \boldsymbol{\alpha}_{3} = \boldsymbol{\alpha}_{2} + \boldsymbol{\alpha}_{3}$ 可知 $\boldsymbol{\alpha}_{2} = 0$ ，而特征向量都是非零向量，矛盾）。

A \boldsymbol{\alpha}_{1} = -\boldsymbol{\alpha}_{1}, \quad A \boldsymbol{\alpha}_{2} = \boldsymbol{\alpha}_{2}

A \boldsymbol{\alpha}_{3} = \boldsymbol{\alpha}_{2} + \boldsymbol{\alpha}_{3} = \boldsymbol{\alpha}_{2} + l_{1} \boldsymbol{\alpha}_{1} + l_{2} \boldsymbol{\alpha}_{2}

A \boldsymbol{\alpha}_{3} = A(l_{1} \boldsymbol{\alpha}_{1} + l_{2} \boldsymbol{\alpha}_{2}) = -l_{1} \boldsymbol{\alpha}_{1} + l_{2} \boldsymbol{\alpha}_{2}

-l_{1} \boldsymbol{\alpha}_{1} + l_{2} \boldsymbol{\alpha}_{2} = \boldsymbol{\alpha}_{2} + l_{1} \boldsymbol{\alpha}_{1} + l_{2} \boldsymbol{\alpha}_{2}, \quad \text{} \quad 2 l_{1} \boldsymbol{\alpha}_{1} + \boldsymbol{\alpha}_{2} = 0

则 $\boldsymbol{\alpha}_{1}$ , $\boldsymbol{\alpha}_{2}$ 线性相关，矛盾。所以 $\boldsymbol{\alpha}_{1}$ , $\boldsymbol{\alpha}_{2}$ , $\boldsymbol{\alpha}_{3}$ 线性无关。

证法二：设存在数 $k_{1}$ , $k_{2}$ , $k_{3}$ ，使得

k_{1} \boldsymbol{\alpha}_{1} + k_{2} \boldsymbol{\alpha}_{2} + k_{3} \boldsymbol{\alpha}_{3} = 0 \quad (1)

用 $A$ 左乘 (1) 的两边，并由 $A \boldsymbol{\alpha}_{1} = -\boldsymbol{\alpha}_{1}$ , $A \boldsymbol{\alpha}_{2} = \boldsymbol{\alpha}_{2}$ 得

-k_{1} \boldsymbol{\alpha}_{1} + (k_{2} + k_{3}) \boldsymbol{\alpha}_{2} + k_{3} \boldsymbol{\alpha}_{3} = 0 \quad (2)

(1) - (2) 得

2 k_{1} \boldsymbol{\alpha}_{1} - k_{3} \boldsymbol{\alpha}_{2} = 0

因为 $\boldsymbol{\alpha}_{1}$ , $\boldsymbol{\alpha}_{2}$ 是 $A$ 的属于不同特征值的特征向量，所以 $\boldsymbol{\alpha}_{1}$ , $\boldsymbol{\alpha}_{2}$ 线性无关，从而 $k_{1} = k_{3} = 0$ 。代入 (1) 得 $k_{2} \boldsymbol{\alpha}_{2} = 0$ ，又由于 $\boldsymbol{\alpha}_{2} \neq 0$ ，所以 $k_{2} = 0$ 。故 $\boldsymbol{\alpha}_{1}$ , $\boldsymbol{\alpha}_{2}$ , $\boldsymbol{\alpha}_{3}$ 线性无关。

(2) 记 $P = (\boldsymbol{\alpha}_{1}, \boldsymbol{\alpha}_{2}, \boldsymbol{\alpha}_{3})$ ，则 $P$ 可逆。

\begin{aligned} A P &= A(\boldsymbol{\alpha}_{1}, \boldsymbol{\alpha}_{2}, \boldsymbol{\alpha}_{3}) = (A \boldsymbol{\alpha}_{1}, A \boldsymbol{\alpha}_{2}, A \boldsymbol{\alpha}_{3}) = (-\boldsymbol{\alpha}_{1}, \boldsymbol{\alpha}_{2}, \boldsymbol{\alpha}_{2} + \boldsymbol{\alpha}_{3}) \\ &= (\boldsymbol{\alpha}_{1}, \boldsymbol{\alpha}_{2}, \boldsymbol{\alpha}_{3}) \begin{pmatrix} -1 & 0 & 0 \\ 0 & 1 & 1 \\ 0 & 0 & 1 \end{pmatrix} = P \begin{pmatrix} -1 & 0 & 0 \\ 0 & 1 & 1 \\ 0 & 0 & 1 \end{pmatrix} \end{aligned}

P^{-1} A P = \begin{pmatrix} -1 & 0 & 0 \\ 0 & 1 & 1 \\ 0 & 0 & 1 \end{pmatrix}

22

（本题满分 11 分）

设随机变量 $X$ 与 $Y$ 相互独立。 $X$ 的概率分布为 $P\{X=i\}=\frac{1}{3}$ $(i=-1,0,1)$ ， $Y$ 的概率密度为

f_{Y}(y)= \begin{cases} 1, & 0 \leq y \leq 1 \\ 0, & \text{} \end{cases}

记 $Z=X+Y$ 。

求 $P\left\{Z \leq \frac{1}{2} \mid X=0\right\}$ ；
求 $Z$ 的概率密度。

概率论与数理统计多维随机变量及其分布边缘分布和条件分布

【答案】

$P\left\{Z \leq \frac{1}{2} \mid X=0\right\} = \frac{1}{2}$
$Z$ 的概率密度函数为
$f_Z(z) = \begin{cases} \frac{1}{3}, & -1 \leq z < 2 \\ 0, & \text{} \end{cases}$

【解析】
(1)

P\left(Z \leq \frac{1}{2} | X=0\right) = P\left(X+Y \leq \frac{1}{2} | X=0\right) = \frac{P\left(X=0, Y \leq \frac{1}{2}\right)}{P(X=0)} = P\left(Y \leq \frac{1}{2}\right) = \int_{0}^{\frac{1}{2}} 1 \, dy = \frac{1}{2}

(2)

\begin{aligned} F_{z}(z) &= P\{Z \leq z\} = P\{X+Y \leq z\} \\ &= P\{X+Y \leq z, X=-\eta\} + P\{X+Y \leq z, X=0\} + P\{X+Y \leq z, X=\eta\} \\ &= P\{Y \leq z+1, X=-\eta\} + P\{Y \leq z, X=0\} + P\{Y \leq z-1, X=\eta\} \\ &= P\{Y \leq z+\eta\} P\{X=-\eta\} + P\{Y \leq z\} P\{X=0\} + P\{Y \leq z-\eta\} P\{X=\eta\} \\ &= \frac{1}{3}\left[P\{Y \leq z+\eta\} + P\{Y \leq z\} + P\{Y \leq z-1\}\right] \\ &= \frac{1}{3}\left[F_{Y}(z+1) + F_{Y}(z) + F_{Y}(z-1)\right] \end{aligned}

f_{z}(z) = \frac{1}{3}\left[f_{Y}(z+1) + f_{Y}(z) + f_{Y}(z-1)\right] = \left\{\begin{array}{ll} \frac{1}{3}, & -1 \leq z < 2 \\ 0, & \text{} \end{array}\right.

23

（本题满分 11 分）

设 $X_{1}, X_{2}, \cdots, X_{n}$ 是总体为 $N(\boldsymbol{\mu}, \boldsymbol{\sigma}^{2})$ 的简单随机样本，记

\bar{X} = \frac{1}{n} \sum_{i=1}^{n} X_{i}, \quad S^{2} = \frac{1}{n-1} \sum_{i=1}^{n} (X_{i} - \bar{X})^{2}

定义统计量

T = \bar{X}^{2} - \frac{1}{n} S^{2}

证明 $T$ 是 $\boldsymbol{\mu}^{2}$ 的无偏估计量。
当 $\boldsymbol{\mu} = 0$ ， $\boldsymbol{\sigma} = 1$ 时，求 $\operatorname{DT}$ 。

概率论与数理统计参数估计与假设检验估计量的无偏性

【答案】

见解析
$D(T) = \frac{2}{n(n-1)}$

【解析】
(1) 因为 $X \sim N(\mu, \sigma^{2})$ ，所以 $\bar{X} \sim N(\mu, \frac{\sigma^{2}}{n})$ ，从而 $E\bar{X}=\mu$ ， $D \bar{X}=\frac{\sigma^{2}}{n}$ 。

\begin{aligned} E(T) &= E\left(\overline{X}^{2}-\frac{1}{n} S^{2}\right) = E \overline{X}^{2} - \frac{1}{n} E\left(S^{2}\right) \\ &= D \overline{X} + (E \overline{X})^{2} - \frac{1}{n} E\left(S^{2}\right) = \frac{1}{n} \sigma^{2} + \mu^{2} - \frac{1}{n} \sigma^{2} = \mu^{2} \end{aligned}

所以， $T$ 是 $\mu^{2}$ 的无偏估计量。

(2)

方法一： $D(T) = E T^{2} - (E T)^{2}$ 。当 $\mu=0$ 时， $E(T)=0$ ， $E\left(S^{2}\right)=\sigma^{2}=1$ 。

\begin{aligned} D(T) &= E T^{2} = E\left(\overline{X}^{4} - \frac{2}{n} \overline{X}^{2} \cdot S^{2} + \frac{S^{4}}{n^{2}}\right) \\ &= E\left(\overline{X}^{4}\right) - \frac{2}{n} E\left(\overline{X}^{2}\right) E\left(S^{2}\right) + \frac{1}{n^{2}} E\left(S^{4}\right) \end{aligned}

因为 $X \sim N(0,1)$ ，所以 $\bar{X} \sim N(0, \frac{1}{n})$ 。

E \bar{X} = 0, \quad D \bar{X} = \frac{1}{n}, \quad E \bar{X}^{2} = D \bar{X} + (E \bar{X})^{2} = \frac{1}{n}

\begin{aligned} E\left(\overline{X}^{4}\right) &= D\left(\overline{X}^{2}\right) + E^{2}\left(\overline{X}^{2}\right) = D\left(\frac{1}{\sqrt{n}} \sqrt{n} \bar{X}\right)^{2} + \left[D(\bar{X}) + E^{2}(\bar{X})\right]^{2} \\ &= \frac{1}{n^{2}} D(\sqrt{n} \bar{X})^{2} + [D(\bar{X})]^{2} = \frac{1}{n^{2}} \times 2 + \left(\frac{1}{n}\right)^{2} = \frac{3}{n^{2}} \end{aligned}

E S^{4} = E\left[\left(S^{2}\right)^{2}\right] = D S^{2} + \left(E S^{2}\right)^{2} = D S^{2} + 1

因为 $W = \frac{(n-1) S^{2}}{\sigma^{2}} = (n-1) S^{2} \sim \chi^{2}(n-1)$ ，所以 $D W = 2(n-1)$ 。又因为 $D W = (n-1)^{2} D S^{2}$ ，所以 $D S^{2} = \frac{2}{(n-1)}$ 。因此，

E S^{4} = \frac{2}{(n-1)} + 1 = \frac{n+1}{n-1}

E T^{2} = \frac{3}{n^{2}} - \frac{2}{n} \cdot \frac{1}{n} \times 1 + \frac{1}{n^{2}} \cdot \frac{n+1}{n-1} = \frac{2}{n(n-1)}

方法二：当 $\mu=0$ ， $\sigma=1$ 时，

\begin{aligned} D(T) &= D\left(\overline{X}^{2} - \frac{1}{n} S^{2}\right) \quad (\text{ }\overline{X} \text{ } S^{2} \text{ }) \\ &= D \overline{X}^{2} + \frac{1}{n^{2}} D S^{2} = \frac{1}{n^{2}} D(\sqrt{n} \overline{X})^{2} + \frac{1}{n^{2}} \cdot \frac{1}{(n-1)^{2}} D\left[(n-1) S^{2}\right] \end{aligned}

由于 $\sqrt{n} \overline{X} \sim N(0,1)$ ，则 $(\sqrt{n} \overline{X})^{2} \sim \chi^{2}(1)$ ，故 $D(\sqrt{n} \overline{X})^{2} = 2$ ，所以

\frac{1}{n^{2}} D(\sqrt{n} \overline{X})^{2} = \frac{2}{n^{2}}

又因为 $(n-1) S^{2} \sim \chi^{2}(n-1)$ ，其方差为 $2(n-1)$ ，所以

\frac{1}{n^{2}} \cdot \frac{1}{(n-1)^{2}} D\left[(n-1) S^{2}\right] = \frac{1}{n^{2}} \cdot \frac{2(n-1)}{(n-1)^{2}} = \frac{2}{n^{2}(n-1)}

因此，

D(T) = \frac{2}{n^{2}} + \frac{2}{n^{2}(n-1)} = \frac{2(n-1) + 2}{n^{2}(n-1)} = \frac{2n}{n^{2}(n-1)} = \frac{2}{n(n-1)}