2016 年真题

选择题

1

设 $a_1 = x (\cos \sqrt{x} - 1)$ ， $a_2 = \sqrt{x} \ln (1 + \sqrt[3]{x})$ ， $a_3 = \sqrt[3]{x + 1} - 1$ ，当 $x \to 0^+$ 时，以上 3 个无穷小量按照从低阶到高阶的排序是（）。

高等数学函数、极限、连续无穷小量的比较

正确答案：B

当 $x \to 0^+$ 时，

a_1 = x(\cos\sqrt{x} - 1) \sim -\frac{1}{2}x^2,

a_2 = \sqrt{x}\ln(1 + \sqrt[3]{x}) \sim x^{\frac{2}{3}},

a_3 = \sqrt[3]{x + 1} - 1 \sim \frac{1}{3}x.

因此，三个无穷小量按照从低阶到高阶的排序为 $a_2, a_3, a_1$ ，故选 B。

2

已知函数 $f(x) = \begin{cases} 2(x - 1), & x < 1, \\ \ln x, & x \geq 1, \end{cases}$ ，则 $f(x)$ 的一个原函数是

高等数学一元函数积分学不定积分的计算

正确答案：D

【解析】
设 $F(x) = \int f(x)dx$ ，由题设得

F(x) = \begin{cases} (x - 1)^2, & x < 1, \\ x\ln x - x + C, & x > 1, \end{cases}

由于 $F(x)$ 连续，需满足

F(1^-) = F(1^+).

代入计算得

(1 - 1)^2 = 1 \cdot \ln 1 - 1 + C \quad \Rightarrow \quad 0 = -1 + C,

因此

C = 1.

3

反常积分 ① $\int_{-\infty}^{0} \frac{1}{x^{2}} e^{\frac{1}{x}} \, dx$ ，② $\int_{0}^{+\infty} \frac{1}{x^{2}} e^{\frac{1}{x}} \, dx$ 的敛散性为

高等数学一元函数积分学反常积分的计算与敛散性

正确答案：B

【解析】
考虑积分 $\int_{-\infty}^{0} \frac{1}{x^2} e^{\frac{1}{x}} dx$ ，
令 $u = \frac{1}{x}$ ，则 $du = -\frac{1}{x^2} dx$ ，
于是原积分化为

\int_{-\infty}^{0} \frac{1}{x^2} e^{\frac{1}{x}} dx = -\int_{-\infty}^{0} e^{\frac{1}{x}} d\left( \frac{1}{x} \right) = -e^{\frac{1}{x}} \Big|_{-\infty}^{0}

代入上下限得

- \left( \lim_{x \to 0^-} e^{\frac{1}{x}} - \lim_{x \to -\infty} e^{\frac{1}{x}} \right) = - (0 - 1) = 1

该积分收敛。

再考虑 $\int_{0}^{+\infty} \frac{1}{x^2} e^{\frac{1}{x}} dx$ ，
类似地有

\int_{0}^{+\infty} \frac{1}{x^2} e^{\frac{1}{x}} dx = -\int_{0}^{+\infty} e^{\frac{1}{x}} d\left( \frac{1}{x} \right) = -e^{\frac{1}{x}} \Big|_{0}^{+\infty}

代入上下限得

- \left( \lim_{x \to +\infty} e^{\frac{1}{x}} - \lim_{x \to 0^+} e^{\frac{1}{x}} \right) = - (1 - \infty) = +\infty

该积分发散。

因此，应选 B。

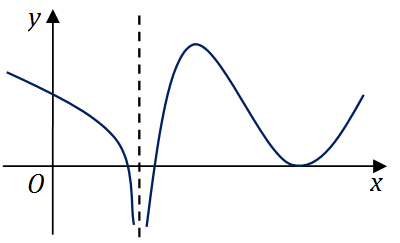
4

设函数 $f(x)$ 在 $(-\infty, +\infty)$ 内连续，其导函数的图形如图所示，则（）

高等数学一元函数微分学函数的单调性、极值与最值

正确答案：B

根据极值的必要条件可知，极值点可能是驻点或导数不存在的点。根据极值的充分条件可知，在某点左右导函数符号发生改变，则该点是极值点。因此从图形可知函数 $f(x)$ 有 2 个极值点。

根据拐点的必要条件可知，拐点可能是二阶导为零的点或二阶导不存在的点。根据拐点的充分条件可知，曲线在某点左右导函数的单调性发生改变，则该点是曲线的拐点。因此曲线 $y = f(x)$ 有 3 个拐点，故选 B。

5

设函数 $f_i(x) \ (i = 1,2)$ 具有二阶连续导数，且 $f_i''(x_0) < 0 \ (i = 1,2)$ ，若两条曲线 $y = f_i(x) \ (i = 1,2)$ 在点 $(x_0,y_0)$ 处具有公切线 $y = g(x)$ ，且在该点处曲线 $y = f_1(x)$ 的曲率大于曲线 $y = f_2(x)$ 的曲率，则在 $x_0$ 的某个邻域内，有（）

高等数学一元函数微分学导数与微分的概念

正确答案：A

【解析】因为 $f_i''(x)$ 连续且 $f_i''(x_0) < 0$ ，根据连续的定义与极限的保号性，在 $x_0$ 的某邻域 $U(x_0)$ 内，有 $f_i''(x) < 0$ ，因此 $f_i(x)$ 在 $U(x_0)$ 内是凸函数。

又因为在 $x = x_0$ 处两曲线具有公切线 $y = g(x)$ ，根据凸函数的几何意义，曲线与切线的位置关系为 $f_i(x) \leq g(x)$ 。

在点 $x_0$ 处， $y = f_1(x)$ 的曲率大于 $y = f_2(x)$ 的曲率，因此 $f_1''(x_0) < f_2''(x_0) < 0$ 。

令 $F(x) = f_1(x) - f_2(x)$ ，由于在 $x = x_0$ 处具有公切线 $y = g(x)$ ，可得 $F(x_0) = 0$ ， $F'(x_0) = 0$ 。

又由 $F''(x_0) < 0$ 可知， $F(x_0) = 0$ 是 $F(x)$ 的极大值，因此在 $x_0$ 的某邻域 $U_1(x_0)$ 内，有 $F(x) \leq 0$ ，即 $f_1(x) \leq f_2(x)$ 。

综合可得 $f_1(x) \leq f_2(x) \leq g(x)$ ，故选 A。

6

已知函数 $f(x, y) = \frac{e^{x}}{x - y}$ ，则

高等数学多元函数微分学偏导数的概念与计算

正确答案：D

由于 $f'_{x}(x,y) = \frac{e^{x}(x - y) - e^{x}}{(x - y)^{2}}$ 和 $f'_{y}(x,y) = \frac{e^{x}}{(x - y)^{2}}$ ，

因此有

f'_{x}(x,y) + f'_{y}(x,y) = \frac{e^{x}(x - y) - e^{x}}{(x - y)^{2}} + \frac{e^{x}}{(x - y)^{2}} = \frac{e^{x}}{x - y} = f(x, y)

故应选 D。

7

设 $A$ ， $B$ 是可逆矩阵，且 $A$ 与 $B$ 相似，则下列结论错误的是

线性代数矩阵的特征值与特征向量

正确答案：C

由于矩阵 $A$ 与 $B$ 相似，存在可逆矩阵 $P$ 使得 $P^{-1}AP = B$ 。

对 $B$ 取转置得：

B^T = P^T A^T (P^T)^{-1} = P^T A^T (P^{-1})^T,

因此 $A^T$ 与 $B^T$ 相似。

对 $B$ 取逆得：

B^{-1} = P^{-1}A^{-1}P,

因此 $A^{-1}$ 与 $B^{-1}$ 相似。

又由 $B = P^{-1}AP$ ，可得：

B^{-1} + B = P^{-1}A^{-1}P + P^{-1}AP = P^{-1}(A^{-1} + A)P,

即 $A + A^{-1}$ 与 $B^{-1} + B$ 相似。

因此正确选项为 C。

8

设二次型 $f(x_1, x_2, x_3) = a(x_1^2 + x_2^2 + x_3^2) + 2x_1x_2 + 2x_2x_3 + 2x_1x_3$ 的正、负惯性指数分别为 $1, 2$ ，则（）

线性代数二次型

正确答案：C

【解析】二次型 $f(x_1,x_2,x_3)$ 对应的矩阵为

A = \begin{pmatrix} a & 1 & 1 \\ 1 & a & 1 \\ 1 & 1 & a \end{pmatrix}.

由

|\lambda E - A| = \begin{vmatrix} \lambda - a & -1 & -1 \\ -1 & \lambda - a & -1 \\ -1 & -1 & \lambda - a \end{vmatrix} = (\lambda - a - 2)(\lambda - a + 1)^2 = 0

可得，矩阵 $A$ 的特征值为

\lambda_1 = a + 2, \quad \lambda_2 = \lambda_3 = a - 1.

由于 $f(x_1,x_2,x_3)$ 的正惯性指数为 1，负惯性指数为 2，且正负惯性指数等于特征值中正、负数的个数，因此有

a + 2 > 0 \quad \text{} \quad a - 1 < 0,

即

-2 < a < 1.

故选 C。

填空题

9

（填空题）曲线 $y = \frac{x^3}{1 + x^2} + \arctan(1 + x^2)$ 的斜渐近线方程为________。

高等数学一元函数微分学曲线的凹凸性、拐点及渐近线

【答案】 $y = x + \frac{\pi}{2}$

【解析】
因为

\begin{gather*} a = \lim_{x \to \infty} \frac{y}{x} = \lim_{x \to \infty} \frac{1}{x} \left( \frac{x^3}{1 + x^2} + \arctan(1 + x^2) \right) = 1, \\ b = \lim_{x \to \infty} (y - a x) = \lim_{x \to \infty} \left( \frac{x^3}{1 + x^2} + \arctan(1 + x^2) - x \right) = \frac{\pi}{2}. \end{gather*}

所以斜渐近线为

y = x + \frac{\pi}{2}.

10

（填空题）极限 $\lim\limits_{n \to \infty} \frac{1}{n^{2}} \left( \sin \frac{1}{n} + 2 \sin \frac{2}{n} + \cdots + n \sin \frac{n}{n} \right) =$ ______。

高等数学一元函数积分学定积分的应用

【答案】 $\sin 1 - \cos 1$

【解析】
因为
$\lim_{n \to \infty} \frac{1}{n^{2}} \left( \sin\frac{1}{n} + 2\sin\frac{2}{n} + \cdots + n\sin\frac{n}{n} \right) = \lim_{n \to \infty} \frac{1}{n} \left( \frac{1}{n} \sin\frac{1}{n} + \frac{2}{n} \sin\frac{2}{n} + \cdots + \frac{n}{n} \sin\frac{n}{n} \right)$

该极限可视为定积分的定义形式，即

\int_{0}^{1} x \sin x \, dx

计算该积分：

\int_{0}^{1} x \sin x \, dx = \sin 1 - \cos 1

因此，原极限值为 $\sin 1 - \cos 1$ 。

11

（填空题）以 $y = x^2 - e^x$ 和 $y = x^2$ 为特解的一阶非齐次线性微分方程为______。

高等数学常微分方程一阶非齐次线性微分方程

【答案】 $y' - y = 2x - x^2$

【解析】 设一阶非齐次线性微分方程为 $y' + p(x)y = q(x)$ 。

根据线性微分方程齐次与非齐次解之间的关系，可知 $x^2 - (x^2 - e^x) = e^x$ 是 $y' + p(x)y = 0$ 的解，因此可得 $p(x) = -1$ 。

又因为 $y = x^2$ 是 $y' + p(x)y = q(x)$ 的解，代入可得 $q(x) = 2x - x^2$ 。

故所求一阶非齐次线性微分方程为 $y' - y = 2x - x^2$ 。

12

（填空题）已知函数 $f(x)$ 在 $(-\infty, +\infty)$ 上连续，且

f(x) = (x + 1)^2 + 2 \int_{0}^{1} f(t) \, dt,

则当 $n \geq 2$ 时， $f^{(n)}(0) =$ ________。

高等数学一元函数积分学变限积分

【答案】 $\frac{5}{2} \times 2^n$

【解析】 当 $x = 0$ 时， $f(0) = 1$ 。

已知

f(x) = (x + 1)^2 + 2 \int_{0}^{1} f(t) \, dt

两边同时对 $x$ 求导，得

f'(x) = 2(x + 1) + 2f(x)

代入 $x = 0$ ，有 $f'(0) = 4$ 。

对

f'(x) = 2(x + 1) + 2f(x)

两边再次对 $x$ 求导，得

f''(x) = 2 + 2f'(x)

代入 $x = 0$ ，有 $f''(0) = 10$ 。

继续对

f''(x) = 2 + 2f'(x)

两边对 $x$ 求导，得

f'''(x) = 2f''(x)

依此类推，可得

f^{(n)}(x) = 2^{n - 2} f''(x)

因此

f^{(n)}(0) = 2^{n - 2} f''(0) = 10 \times 2^{n - 2} = \frac{5}{2} \times 2^n

13

（填空题）已知动点 $P$ 在曲线 $y = x^3$ 上运动，记坐标原点与点 $P$ 间的距离为 $l$ 。若点 $P$ 的横坐标对时间的变化率为常数 $v_0$ ，则当点 $P$ 运动到点 $(1,1)$ 时， $l$ 对时间的变化率是______。

高等数学一元函数微分学导数与微分的计算

【答案】 $2\sqrt{2}v_0$

【解析】 设 $l = \sqrt{x^2 + y^2} = \sqrt{x^2 + x^6}$ ，对 $t$ 求导得：

\frac{dl}{dt} = \frac{dl}{dx} \cdot \frac{dx}{dt} = \frac{2x + 6x^5}{2\sqrt{x^2 + x^6}} \cdot \frac{dx}{dt}.

当 $x = 1$ 时，已知 $\frac{dx}{dt} = v_0$ ，代入得：

\left. \frac{dl}{dt} \right|_{x=1} = \frac{2 + 6}{2\sqrt{1 + 1}} \cdot v_0 = \frac{8}{2\sqrt{2}} v_0 = 2\sqrt{2}v_0.

14

（填空题）设矩阵 $\begin{bmatrix} a & -1 & -1 \\ -1 & a & -1 \\ -1 & -1 & a \end{bmatrix}$ 与 $\begin{bmatrix} 1 & 1 & 0 \\ 0 & -1 & 1 \\ 1 & 0 & 1 \end{bmatrix}$ 等价，则 $a =$ ______。

线性代数矩阵矩阵的秩

【答案】 2

【解析】 首先计算矩阵 $B$ 的行列式：

|B| = \begin{vmatrix} 1 & 1 & 0 \\ 0 & -1 & 1 \\ 1 & 0 & 1 \end{vmatrix} = 0

因此 $r(B) = 2$ 。

接着计算矩阵 $A$ 的行列式：

|A| = \begin{vmatrix} a & -1 & -1 \\ -1 & a & -1 \\ -1 & -1 & a \end{vmatrix} = (a + 1)^2 (a - 2) = 0

当 $a = -1$ 时， $r(A) = 1$ ；当 $a = 2$ 时， $r(A) = 2$ 。因此 $a = 2$ 。

解答题

15

（本题满分 10 分）求极限

\lim_{x \to 0} \left( \cos 2x + 2x \sin x - 1 \right)^{\frac{1}{x^4}}

高等数学函数、极限、连续函数极限的计算

【答案】 $e^{\frac{1}{3}}$

【解析】
原极限可表示为

\lim_{x \to 0} \left( \cos 2x + 2x \sin x - 1 \right)^{\frac{1}{x^4}} = e^{\lim\limits_{x \to 0} \frac{1}{x^4} \left( \cos 2x + 2x \sin x - 1 \right)}.

其中，

\begin{align*} &\lim_{x \to 0} \frac{1}{x^4} \left( \cos 2x + 2x \sin x - 1 \right) \\ &= \lim_{x \to 0} \frac{1 - \frac{1}{2}(2x)^2 + \frac{1}{4!}(2x)^4 + o(x^4) + 2x \left( x - \frac{x^3}{3!} + o(x^3) \right) - 1}{x^4} \\ &= \lim_{x \to 0} \frac{1 - 2x^2 + \frac{2}{3}x^4 + 2x^2 - \frac{x^4}{3} + o(x^4) - 1}{x^4} \\ &= \lim_{x \to 0} \frac{\frac{1}{3}x^4 + o(x^4)}{x^4} \\ &= \frac{1}{3}. \end{align*}

因此，原极限

= e^{\frac{1}{3}}.

16

（本题满分 10 分）

设函数 $f(x) = \int_{0}^{1} |t^2 - x^2| \, \mathrm{d}t \ (x > 0)$ ，求 $f'(x)$ 并求 $f(x)$ 的最小值。

高等数学一元函数积分学变限积分

【答案】
$f'(x) = \begin{cases} 4x^2 - 2x & 0 < x \leq 1 \\ 2x & x > 1 \end{cases}$
$f(x)$ 的最小值为 $\frac{1}{4}$ 。

【解析】
$f(x) = \int_{0}^{1} |t^2 - x^2| \, \mathrm{d}t \quad (x > 0)$

当 $0 < x \leq 1$ 时，

\begin{align*} f(x) &= \int_{0}^{x} (x^2 - t^2) \, \mathrm{d}t + \int_{x}^{1} (t^2 - x^2) \, \mathrm{d}t \\ &= x^3 - \frac{1}{3}x^3 + \frac{1}{3} - \frac{1}{3}x^3 - x^2(1 - x) \\ &= \frac{4}{3}x^3 - x^2 + \frac{1}{3} \end{align*}

当 $x > 1$ 时，

f(x) = \int_{0}^{1} (x^2 - t^2) \, \mathrm{d}t = x^2 \int_{0}^{1} \mathrm{d}t - \int_{0}^{1} t^2 \, \mathrm{d}t = x^2 - \frac{1}{3}

即

f(x) = \begin{cases} \frac{4}{3}x^3 - x^2 + \frac{1}{3} & 0 < x \leq 1 \\ x^2 - \frac{1}{3} & x > 1 \end{cases}

f'(x) = \begin{cases} 4x^2 - 2x & 0 < x \leq 1 \\ 2x & x > 1 \end{cases}

令 $f'(x) = 0$ ，可得当 $0 < x \leq 1$ 时 $x = \frac{1}{2}$ 为驻点且为极小值点， $f\left(\frac{1}{2}\right) = \frac{1}{4}$ ，而 $f(1) = \frac{2}{3}$ 。

因此， $f(x)$ 的最小值为 $\frac{1}{4}$ 。

17

（本题满分 10 分）

已知函数 $z = z(x, y)$ 由方程 $(x^2 + y^2)z + \ln z + 2(x + y + 1) = 0$ 确定，求 $z = z(x, y)$ 的极值。

高等数学多元函数微分学多元函数的极值问题

【答案】 在点 $(-1, -1)$ 处取得极大值，极大值为 $z = 1$ 。

【解析】

给定方程组：

\begin{cases} 2xz + x^2 \frac{\partial z}{\partial x} + y^2 \frac{\partial z}{\partial x} + \frac{1}{z} \frac{\partial z}{\partial x} + 2 = 0 \\ x^2 \frac{\partial z}{\partial y} + 2yz + y^2 \frac{\partial z}{\partial y} + \frac{1}{z} \frac{\partial z}{\partial y} + 2 = 0 \end{cases}

整理可得：

\begin{cases} xz + 1 = 0 \\ yz + 1 = 0 \\ x^2 z + y^2 z + \ln z + 2(x + y + 1) = 0 \end{cases} \Rightarrow \begin{cases} x = -1 \\ y = -1 \\ z = 1 \end{cases}

由第一个方程 $2xz + x^2 \frac{\partial z}{\partial x} + y^2 \frac{\partial z}{\partial x} + \frac{1}{z} \frac{\partial z}{\partial x} + 2 = 0$ 再对 $x$ 求导得：

2z + 2x \frac{\partial z}{\partial x} + (x^2 + y^2) \frac{\partial^2 z}{\partial x^2} - \frac{1}{z^2} \left( \frac{\partial z}{\partial x} \right)^2 + \frac{1}{z} \cdot \frac{\partial^2 z}{\partial x^2} = 0

代入 $\frac{\partial z}{\partial x} = 0$ ， $x = -1$ ， $y = -1$ ， $z = 1$ ，得：

A = \frac{\partial^2 z}{\partial x^2} = -\frac{2}{3} < 0

同理可得 $\frac{\partial^2 z}{\partial y^2} < 0$ 。

由第一个方程对 $y$ 求导得：

2x \frac{\partial z}{\partial y} + 2y \frac{\partial z}{\partial x} + (x^2 + y^2) \frac{\partial^2 z}{\partial x \partial y} - \frac{1}{z^2} \cdot \frac{\partial z}{\partial x} \cdot \frac{\partial z}{\partial y} + \frac{1}{z} \cdot \frac{\partial^2 z}{\partial x \partial y} = 0

代入 $\frac{\partial z}{\partial x} = 0$ ， $\frac{\partial z}{\partial y} = 0$ ， $x = -1$ ， $y = -1$ ， $z = 1$ ，得：

\frac{\partial^2 z}{\partial x \partial y} = 0

由于 $AC - B^2 > 0$ 且 $A < 0$ ，故在点 $(-1, -1)$ 处取得极大值。

18

（本题满分 10 分）

设 $D$ 是由直线 $y = 1$ 、 $y = x$ 、 $y = -x$ 围成的有界区域，计算二重积分

\iint\limits_{D} \frac{x^2 - xy - y^2}{x^2 + y^2} \, dx \, dy

高等数学多元函数积分学重积分的计算

【答案】 $1 - \frac{\pi}{2}$

【解析】
【解析】
$I = \iint\limits_{D} \frac{x^2 - xy - y^2}{x^2 + y^2} \, dx \, dy = \iint\limits_{D} \frac{x^2 + y^2 - 2y^2}{x^2 + y^2} \, dx \, dy - \iint\limits_{D} \frac{xy}{x^2 + y^2} \, dx \, dy = I_1 + I_2$

由于区域 $D$ 关于 $y$ 轴对称，可知 $I_2 = 0$ 。

进一步计算：

I_1 = \iint\limits_{D} dx \, dy - 2 \iint\limits_{D} \frac{y^2}{x^2 + y^2} \, dx \, dy = I_3 + I_4

其中：

I_3 = \iint\limits_{D} dx \, dy = 1

I_4 = 2 \iint\limits_{D} \frac{y^2}{x^2 + y^2} \, dx \, dy = 4 \iint\limits_{D_1} \frac{y^2}{x^2 + y^2} \, dx \, dy = 4 \int_{0}^{1} dy \int_{0}^{y} \frac{y^2}{x^2 + y^2} \, dx

计算内层积分：

\int_{0}^{y} \frac{y^2}{x^2 + y^2} \, dx = y^2 \int_{0}^{y} \frac{1}{\left( \frac{x}{y} \right)^2 + 1} \cdot \frac{dx}{y} = y \left[ \arctan \frac{x}{y} \right]_{0}^{y} = \frac{\pi}{4} y

代入得：

I_4 = \pi \int_{0}^{1} y \, dy = \frac{\pi}{2}

因此：

I = 1 - \frac{\pi}{2}

19

（本题满分 10 分）

已知 $y_1(x) = e^x$ ， $y_2(x) = \mu(x) e^x$ 是二阶微分方程

(2x - 1) y'' - (2x + 1) y' + 2y = 0

的两个解，若 $\mu(-1) = e$ ， $\mu(0) = -1$ ，求 $\mu(x)$ 并写出该微分方程的通解。

高等数学常微分方程常系数非齐次线性微分方程

【答案】
$\mu(x) = -2xe^{-x} - e^{-x}$ ，该微分方程的通解为 $y = k_1e^x + k_2(-2x - 1)e^{-x}$ ，其中 $k_1, k_2$ 为任意常数。

【解析】
已知 $y_2(x) = \mu(x)e^x$ 是二阶微分方程

(2x - 1)y'' - (2x + 1)y' + 2y = 0

的一个解。将其代入方程并整理可得

(2x - 1)\mu'' = (3 - 2x)\mu',

即

\frac{\mu''}{\mu'} = \frac{3 - 2x}{2x - 1}.

两边积分得

\int \frac{\mu''}{\mu'}dx = \int \frac{3 - 2x}{2x - 1}dx,

\ln|\mu'| = \int \frac{-2x + 3}{2x - 1}dx = -x + \ln|2x - 1| + \ln C_1,

因此

|\mu'(x)| = e^{-x}|2x - 1|C_1,

取

\mu'(x) = C_1(2x - 1)e^{-x}.

进一步积分得

\mu(x) = \int C_1(2x - 1)e^{-x}dx = C_1\left[-2xe^{-x} - e^{-x} + C_2\right].

由已知条件 $\mu(-1) = e$ ， $\mu(0) = -1$ ，解得 $C_1 = 1$ ， $C_2 = 0$ ，
所以

\mu(x) = -2xe^{-x} - e^{-x}.

已知 $y_1(x)$ 与 $y_2(x)$ 线性无关，因此原方程的通解为

y = k_1e^x + k_2(-2x - 1)e^{-x},

其中 $k_1, k_2$ 为任意常数。

20

（本题满分 11 分）

设 $D$ 是由曲线 $y = \sqrt{1 - x^2} \ (0 \leq x \leq 1)$ 与参数方程

\begin{cases} x = \cos^3 t \\ y = \sin^3 t \end{cases} \quad (0 \leq t \leq \frac{\pi}{2})

围成的平面区域，求 $D$ 绕 $x$ 轴旋转一周所得旋转体的体积和表面积。

高等数学一元函数积分学定积分的应用

【答案】
体积： $\frac{18\pi}{35}$ ，表面积： $\frac{16\pi}{5}$

【解析】
体积部分

体积计算公式为：

V = V_1 - V_2 = \pi \int_{0}^{1} (1 - x^2) \, dx - \pi \int_{0}^{\frac{\pi}{2}} \sin^6 t \cdot 3\cos^2 t (-\sin t) \, dt

化简得：

V = \frac{2\pi}{3} - 3\pi \int_{0}^{\frac{\pi}{2}} \sin^7 t (1 - \sin^2 t) \, dt + 3\pi \int_{0}^{\frac{\pi}{2}} \sin^9 t \, dt

计算得：

V = \frac{2\pi}{3} - 3\pi \cdot \frac{16}{35} \cdot \frac{1}{9} = \frac{18}{35}\pi

表面积部分

对于曲线 $y = \sqrt{1 - x^2} \ (0 \leq x \leq 1)$ 旋转所得表面积 $S_1$ ：

S_1 = 2\pi \int_{0}^{1} y \sqrt{1 + y'^2(x)} \, dx = 2\pi \int_{0}^{1} \sqrt{1 - x^2} \sqrt{1 + \frac{x^2}{1 - x^2}} \, dx = 2\pi

对于参数方程

\begin{cases} x = \cos^3 t \\ y = \sin^3 t \end{cases} \quad (0 \leq t \leq \frac{\pi}{2})

旋转所得表面积 $S_2$ ：

\begin{align*} S_2 &= 2\pi \int_{0}^{\frac{\pi}{2}} \sin^3 t \sqrt{(3\sin^2 t \cos t)^2 + (3\cos^2 t \sin t)^2} \, dt \\ &= 2\pi \int_{0}^{\frac{\pi}{2}} \sin^3 t \cdot 3\sin t \cos t \, dt \\ &= 2\pi \int_{0}^{\frac{\pi}{2}} 3\sin^4 t \cos t \, dt \\ &= \frac{6\pi}{5} \sin^5 t \Big|_{0}^{\frac{\pi}{2}} \\ &= \frac{6\pi}{5}. \end{align*}

总表面积为：

S = S_1 + S_2 = 2\pi + \frac{6\pi}{5} = \frac{16\pi}{5}

21

（本题满分 11 分）

已知 $f(x)$ 在 $[0, \frac{3\pi}{2}]$ 上连续，在 $(0, \frac{3\pi}{2})$ 内是函数 $\frac{\cos x}{2x - 3\pi}$ 的一个原函数，且 $f(0) = 0$ ，

（1）求 $f(x)$ 在区间 $[0, \frac{3\pi}{2}]$ 上的平均值；

（2）证明 $f(x)$ 在区间 $(0, \frac{3\pi}{2})$ 内存在唯一零点。

高等数学一元函数积分学定积分的应用

【答案】
（1） $\frac{1}{3\pi}$
（2）见解析

【解析】
（1）函数 $f(x) = \int_{0}^{x} \frac{\cos t}{2t - 3\pi} dt$ 。根据平均值公式， $f(x)$ 在区间 $[0, \frac{3\pi}{2}]$ 上的平均值为

\frac{\int_{0}^{\frac{3\pi}{2}} f(x) dx}{\frac{3\pi}{2}}

利用交换积分次序，

\int_{0}^{\frac{3\pi}{2}} dx \int_{0}^{x} \frac{\cos t}{2t - 3\pi} dt = \int_{0}^{\frac{3\pi}{2}} dt \int_{t}^{\frac{3\pi}{2}} \frac{\cos t}{2t - 3\pi} dx

计算内层积分：

\int_{t}^{\frac{3\pi}{2}} \frac{\cos t}{2t - 3\pi} dx = \frac{\cos t}{2t - 3\pi} \cdot \left( \frac{3\pi}{2} - t \right)

因此平均值为

\frac{\int_{0}^{\frac{3\pi}{2}} \frac{\cos t}{2t - 3\pi} \cdot \left( \frac{3\pi}{2} - t \right) dt}{\frac{3\pi}{2}} = \frac{-\int_{0}^{\frac{3\pi}{2}} \frac{\cos t}{2} dt}{\frac{3\pi}{2}}

计算定积分：

-\frac{1}{2} \sin t \Big|_{0}^{\frac{3\pi}{2}} = -\frac{1}{2} (-1 - 0) = \frac{1}{2}

故平均值为

\frac{\frac{1}{2}}{\frac{3\pi}{2}} = \frac{1}{3\pi}

（2）由 $f(x) = \int_{0}^{x} \frac{\cos t}{2t - 3\pi} dt$ ，求导得

f'(x) = \frac{\cos x}{2x - 3\pi}

令 $f'(x) = 0$ ，解得在区间 $(0, \frac{3\pi}{2})$ 上的唯一驻点为 $x = \frac{\pi}{2}$ 。

当 $0 < x < \frac{\pi}{2}$ 时， $\cos x > 0$ ， $2x - 3\pi < 0$ ，故 $f'(x) < 0$ ；
当 $\frac{\pi}{2} < x < \frac{3\pi}{2}$ 时， $\cos x < 0$ ， $2x - 3\pi < 0$ ，故 $f'(x) > 0$ 。

因此 $x = \frac{\pi}{2}$ 为 $f(x)$ 在区间 $(0, \frac{3\pi}{2})$ 内的极小值点，也是最小值点，即 $f_{\text{min}}(x) = f\left( \frac{\pi}{2} \right) < 0$ 。

又 $f(0) = 0$ ，计算 $f\left( \frac{3\pi}{2} \right) = \int_{0}^{\frac{3\pi}{2}} \frac{\cos t}{2t - 3\pi} dt$ 。令 $u = 2t - 3\pi$ ，则 $t = \frac{u + 3\pi}{2}$ ， $dt = \frac{1}{2} du$ 。当 $t = 0$ 时 $u = -3\pi$ ， $t = \frac{3\pi}{2}$ 时 $u = 0$ ，积分变为

\frac{1}{2} \int_{-3\pi}^{0} \frac{\cos \frac{u + 3\pi}{2}}{u} du = \frac{1}{2} \int_{-3\pi}^{0} \frac{-\sin \frac{u}{2}}{u} du > 0

（可通过积分性质判断符号）。

结合单调性： $f(x)$ 在区间 $(0, \frac{\pi}{2})$ 上单调递减，且 $f(0) = 0$ ，故该区间内无零点；在区间 $(\frac{\pi}{2}, \frac{3\pi}{2})$ 上单调递增，且 $f\left( \frac{\pi}{2} \right) < 0$ ， $f\left( \frac{3\pi}{2} \right) > 0$ ，故该区间内有唯一零点。

综上所述， $f(x)$ 在区间 $(0, \frac{3\pi}{2})$ 内只有唯一零点。

22

（本题满分 11 分）

设矩阵 $A = \begin{pmatrix} 1 & 1 & 1 - a \\ 1 & 0 & a \\ a + 1 & 1 & a + 1 \end{pmatrix}$ ， $\boldsymbol{\beta} = \begin{pmatrix} 0 \\ 1 \\ 2a - 2 \end{pmatrix}$ ，且方程组 $A \boldsymbol{x} = \boldsymbol{\beta}$ 无解，

（1）求 $a$ 的值；

（2）求方程组 $A^T A \boldsymbol{x} = A^T \boldsymbol{\beta}$ 的通解。

线性代数线性方程组

【答案】
（1） $a = 0$
（2） $\boldsymbol{x} = k \begin{pmatrix} 0 \\ -1 \\ 1 \end{pmatrix} + \begin{pmatrix} 1 \\ -2 \\ 0 \end{pmatrix}, \quad k \in \mathbb{R}$

【解析】
（1）由方程组 $A\boldsymbol{x} = \boldsymbol{\beta}$ 无解，可知 $r(A) \neq r(A, \boldsymbol{\beta})$ ，因此 $|A| = 0$ 。
计算行列式：

|A| = \begin{vmatrix} 1 & 1 & 1 - a \\ 1 & 0 & a \\ a + 1 & 1 & a + 1 \end{vmatrix} = 0

解得 $a = 0$ 或 $a = 2$ 。
当 $a = 0$ 时， $r(A) \neq r(A, \boldsymbol{\beta})$ ；当 $a = 2$ 时， $r(A) = r(A, \boldsymbol{\beta})$ 。因此 $a = 0$ 符合题意。

（2）当 $a = 0$ 时，

A^T A = \begin{pmatrix} 3 & 2 & 2 \\ 2 & 2 & 2 \\ 2 & 2 & 2 \end{pmatrix}, \quad A^T \boldsymbol{\beta} = \begin{pmatrix} -1 \\ -2 \\ -2 \end{pmatrix}

于是

(A^T A, A^T \boldsymbol{\beta}) = \begin{pmatrix} 3 & 2 & 2 & -1 \\ 2 & 2 & 2 & -2 \\ 2 & 2 & 2 & -2 \end{pmatrix} \to \begin{pmatrix} 1 & 0 & 0 & 1 \\ 0 & 1 & 1 & -2 \\ 0 & 0 & 0 & 0 \end{pmatrix}

因此，方程组 $A^T A\boldsymbol{x} = A^T \boldsymbol{\beta}$ 的通解为：

\boldsymbol{x} = k \begin{pmatrix} 0 \\ -1 \\ 1 \end{pmatrix} + \begin{pmatrix} 1 \\ -2 \\ 0 \end{pmatrix}, \quad k \in \mathbb{R}

23

（本题满分 11 分）

已知矩阵

A = \begin{pmatrix} 0 & -1 & 1 \\ 2 & -3 & 0 \\ 0 & 0 & 0 \end{pmatrix}

（1）求 $A^{99}$

（2）设 3 阶矩阵 $B = (\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \boldsymbol{\alpha}_3)$ 满足 $B^2 = BA$ 。记 $B^{100} = (\boldsymbol{\beta}_1, \boldsymbol{\beta}_2, \boldsymbol{\beta}_3)$ ，将 $\boldsymbol{\beta}_1, \boldsymbol{\beta}_2, \boldsymbol{\beta}_3$ 分别表示为 $\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \boldsymbol{\alpha}_3$ 的线性组合。

线性代数矩阵矩阵的运算与变换

【答案】
(1)

A^{99} = \begin{pmatrix} -2 + 2^{99} & 1 - 2^{99} & 2 - 2^{99} \\ -2 + 2^{100} & 1 - 2^{100} & 2 - 2^{99} \\ 0 & 0 & 0 \end{pmatrix}

(2)

\boldsymbol{\beta}_1 = (-2 + 2^{99})\boldsymbol{\alpha}_1 + (-2 + 2^{100})\boldsymbol{\alpha}_2

\boldsymbol{\beta}_2 = (1 - 2^{99})\boldsymbol{\alpha}_1 + (1 - 2^{100})\boldsymbol{\alpha}_2

\boldsymbol{\beta}_3 = (2 - 2^{99})\boldsymbol{\alpha}_1 + (2 - 2^{99})\boldsymbol{\alpha}_2

【解析】
(1) 由 $|\lambda E - A| = \lambda(\lambda + 1)(\lambda + 2) = 0$ ，得 $\lambda_1 = 0, \lambda_2 = -1, \lambda_3 = -2$ 。
因此 $A$ 可相似对角化，且 $A$ 与

\begin{pmatrix} 0 & & \\ & -1 & \\ & & -2 \end{pmatrix}

相似。
由 $(0E - A)\boldsymbol{x} = \boldsymbol{0}$ 得 $\boldsymbol{\eta}_1 = \begin{pmatrix} \frac{3}{2} \\ 1 \\ 1 \end{pmatrix}$ ；
由 $(-E - A)\boldsymbol{x} = \boldsymbol{0}$ 得 $\boldsymbol{\eta}_2 = \begin{pmatrix} 1 \\ 1 \\ 0 \end{pmatrix}$ ；
由 $(-2E - A)\boldsymbol{x} = \boldsymbol{0}$ 得 $\boldsymbol{\eta}_3 = \begin{pmatrix} 1 \\ 2 \\ 0 \end{pmatrix}$ 。
令 $P = \begin{pmatrix} \frac{3}{2} & 1 & 1 \\ 1 & 1 & 2 \\ 1 & 0 & 0 \end{pmatrix}$ ，则

P^{-1}AP = \begin{pmatrix} 0 & & \\ & -1 & \\ & & -2 \end{pmatrix} = \Lambda

因此 $A = P\Lambda P^{-1}$ ，可得

A^{99} = P\Lambda^{99} P^{-1} = \begin{pmatrix} -2 + 2^{99} & 1 - 2^{99} & 2 - 2^{99} \\ -2 + 2^{100} & 1 - 2^{100} & 2 - 2^{99} \\ 0 & 0 & 0 \end{pmatrix}

(2) 由 $B^2 = BA$ 得

B^3 = B^2A = BA^2 \Rightarrow B^4 = B^2A^2 = BA^3 \Rightarrow \cdots \Rightarrow B^{100} = BA^{99}

因此

(\boldsymbol{\beta}_1\ \boldsymbol{\beta}_2\ \boldsymbol{\beta}_3) = (\boldsymbol{\alpha}_1\ \boldsymbol{\alpha}_2\ \boldsymbol{\alpha}_3)A^{99}

于是

\boldsymbol{\beta}_1 = (-2 + 2^{99})\boldsymbol{\alpha}_1 + (-2 + 2^{100})\boldsymbol{\alpha}_2

\boldsymbol{\beta}_2 = (1 - 2^{99})\boldsymbol{\alpha}_1 + (1 - 2^{100})\boldsymbol{\alpha}_2

\boldsymbol{\beta}_3 = (2 - 2^{99})\boldsymbol{\alpha}_1 + (2 - 2^{99})\boldsymbol{\alpha}_2