2010 年真题

选择题

1

函数 $f (x) = \frac{x ^{2} - x}{x ^{2} - 1} 1 + \frac{1}{x ^{2}}$ 的无穷间断点的个数为

正确答案：B

函数 $f (x) = \frac{x ^{2} - x}{x ^{2} - 1} 1 + \frac{1}{x ^{2}}$ 有间断点 $x = 0, 1, - 1$ 。

因为

x \to 0 lim f (x) = x \to 0 lim \frac{x ( x - 1 )}{( x + 1 ) ( x - 1 )} 1 + \frac{1}{x ^{2}} = x \to 0 lim x 1 + \frac{1}{x ^{2}},

其中

x \to 0^{+} lim x 1 + \frac{1}{x ^{2}} = 1, x \to 0^{-} lim x 1 + \frac{1}{x ^{2}} = - 1,

所以 $x = 0$ 为跳跃间断点。

虽然

x \to 1 lim f (x) = \frac{1}{2} 1 + 1 = \frac{2}{2},

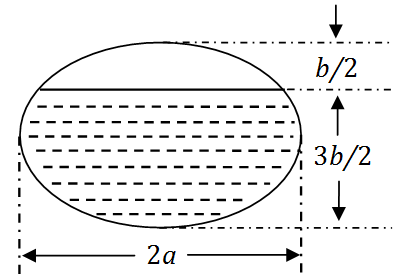
所以 $x = 1$ 为可去间断点。

而

x \to - 1 lim f (x) = x \to - 1 lim \frac{x ( x - 1 )}{( x + 1 ) ( x - 1 )} 1 + \frac{1}{x ^{2}} = \infty,

即 $x = - 1$ 为无穷间断点。

故无穷间断点个数为 1。

2

设 $y_{1}$ 、 $y_{2}$ 是一阶线性非齐次微分方程 $y^{'} + p (x) y = q (x)$ 的两个特解，若常数 $λ$ 、 $μ$ 使 $λ y_{1} + μ y_{2}$ 是该方程的解， $λ y_{1} - μ y_{2}$ 是该方程对应的齐次方程的解，则（）

正确答案：A

由于 $λ y_{1} - μ y_{2}$ 是 $y^{'} + P (x) y = 0$ 的解，因此有

(λ y_{1} - μ y_{2})^{'} + P (x) (λ y_{1} - μ y_{2}) = 0,

即

λ (y_{1}^{'} + P (x) y_{1}) - μ (y_{2}^{'} + P (x) y_{2}) = 0.

又已知

y_{1}^{'} + P (x) y_{1} = q (x), y_{2}^{'} + P (x) y_{2} = q (x),

代入得

λ q (x) - μ q (x) = 0 \Rightarrow (λ - μ) q (x) = 0. (1)

由于一阶非齐次微分方程 $y^{'} + p (x) y = q (x)$ 是非齐次的，可知 $q (x) \neq = 0$ ，因此

λ - μ = 0.

又因为 $λ y_{1} + μ y_{2}$ 是非齐次微分方程 $y^{'} + P (x) y = q (x)$ 的解，所以

(λ y_{1} + μ y_{2})^{'} + P (x) (λ y_{1} + μ y_{2}) = q (x),

整理得

λ (y_{1}^{'} + P (x) y_{1}) + μ (y_{2}^{'} + P (x) y_{2}) = q (x),

即

(λ + μ) q (x) = q (x) .

由 $q (x) \neq = 0$ 可得

λ + μ = 1. (2)

由 (1) 与 (2) 解得

λ = μ = \frac{1}{2} .

故应选 (A)。

3

曲线 $y = x^{2}$ 与曲线 $y = a ln x (a \neq = 0)$ 相切，则 $a = ()$

正确答案：C

由于曲线 $y = x^{2}$ 与曲线 $y = a ln x (a \neq = 0)$ 相切，在切点处两条曲线的斜率相等，即

2 x = \frac{a}{x},

解得

x = \frac{a}{2} (x > 0) .

在切点处两条曲线的纵坐标也相等。对于 $y = x^{2}$ ，当 $x = \frac{a}{2}$ 时，

y = \frac{a}{2} .

对于 $y = a ln x$ ，当 $x = \frac{a}{2}$ 时，

y = a ln \frac{a}{2} = \frac{a}{2} ln \frac{a}{2} .

因此有

\frac{a}{2} = \frac{a}{2} ln \frac{a}{2} .

解得

a = 2 e .

故正确答案为 (C)。

4

设 $m, n$ 是正数，反常积分 $\int_{0}^{1} \frac{m l n ^{2} ( 1 - x )}{n x} d x$ （）

正确答案：D

$x = 0$ 与 $x = 1$ 都是瑕点，应分成

\int_{0}^{1} \frac{m ln ^{2} ( 1 - x )}{n x} d x = \int_{0}^{\frac{1}{2}} \frac{m ln ^{2} ( 1 - x )}{n x} d x + \int_{\frac{1}{2}}^{1} \frac{m ln ^{2} ( 1 - x )}{n x} d x .

对于 $\int_{0}^{\frac{1}{2}} \frac{m l n ^{2} ( 1 - x )}{n x} d x$ ，当 $x \to 0^{+}$ 时， $ln (1 - x) \sim - x$ ，故 $m ln^{2} (1 - x) \sim m x^{2} = x^{\frac{2}{m}}$ ，则被积函数等价于 $\frac{x ^{\frac{2}{m}}}{x ^{\frac{1}{n}}} = x^{\frac{2}{m} - \frac{1}{n}}$ 。

根据反常积分收敛性判别法，当 $\frac{2}{m} - \frac{1}{n} > - 1$ 时收敛，否则发散。但无论 $m, n$ 取何正整数，该积分的收敛性仅由指数决定。而题目问的是积分本身是否与 $m, n$ 有关。

实际计算中，对于 $\int_{0}^{\frac{1}{2}} \frac{m l n ^{2} ( 1 - x )}{n x} d x$ ，当 $x \to 0^{+}$ 时， $lim_{x \to 0^{+}} \frac{[ l n ^{2} ( 1 - x ) ] ^{\frac{1}{m}}}{x ^{\frac{1}{n}}}$ 的极限为有限值，故积分收敛性与 $m, n$ 无关。

对于 $\int_{\frac{1}{2}}^{1} \frac{m l n ^{2} ( 1 - x )}{n x} d x$ ，当 $x \to 1^{-}$ 时，令 $t = 1 - x$ ，则积分变为 $\int_{0}^{\frac{1}{2}} \frac{m l n ^{2} t}{n 1 - t} d t$ 。此时 $n 1 - t \sim 1$ ，故被积函数等价于 $m ln^{2} t$ ，而 $ln t \sim t - 1$ ，即 $m ln^{2} t \sim m (t - 1)^{2}$ ，在 $t \to 0^{+}$ 时，积分收敛性同样与 $m, n$ 无关。

综上，该反常积分与 $m, n$ 取值都无关。

5

设函数 $z = z (x, y)$ ，由方程 $F (\frac{y}{x}, \frac{z}{x}) = 0$ 确定，其中 $F$ 为可微函数，且 $F_{2}^{'} \neq = 0$ ，则

x \frac{\partial z}{\partial x} + y \frac{\partial z}{\partial y} = ()

正确答案：B

根据隐函数求导公式，有：

\frac{\partial z}{\partial x} = - \frac{F _{x}^{'}}{F _{z}^{'}} = - \frac{F _{1}^{'} \cdot ( - \frac{y}{x ^{2}} ) + F _{2}^{'} \cdot ( - \frac{z}{x ^{2}} )}{F _{2}^{'} \cdot \frac{1}{x}} = \frac{F _{1}^{'} \cdot \frac{y}{x} + F _{2}^{'} \cdot \frac{z}{x}}{F _{2}^{'}} = \frac{y F _{1}^{'} + z F _{2}^{'}}{x F _{2}^{'}},

\frac{\partial z}{\partial y} = - \frac{F _{y}^{'}}{F _{z}^{'}} = - \frac{F _{1}^{'} \cdot \frac{1}{x}}{F _{2}^{'} \cdot \frac{1}{x}} = - \frac{F _{1}^{'}}{F _{2}^{'}} .

因此，

x \frac{\partial z}{\partial x} + y \frac{\partial z}{\partial y} = \frac{y F _{1}^{'} + z F _{2}^{'}}{F _{2}^{'}} - \frac{y F _{1}^{'}}{F _{2}^{'}} = \frac{z F _{2}^{'}}{F _{2}^{'}} = z .

6

n \to \infty lim i = 1 \sum n j = 1 \sum n \frac{n}{( n + i ) ( n ^{2} + j ^{2} )} = ()

正确答案：D

i = 1 \sum n j = 1 \sum n \frac{n}{( n + i ) ( n ^{2} + j ^{2} )} = i = 1 \sum n \frac{1}{n + i} (j = 1 \sum n \frac{n}{n ^{2} + j ^{2}}) = (i = 1 \sum n \frac{n}{n + i}) (j = 1 \sum n \frac{1}{n ^{2} + j ^{2}})

n \to \infty lim j = 1 \sum n \frac{n}{n ^{2} + j ^{2}} = n \to \infty lim \frac{1}{n} j = 1 \sum n \frac{1}{1 + ( \frac{j}{n} ) ^{2}} = \int_{0}^{1} \frac{1}{1 + y ^{2}} d y

n \to \infty lim i = 1 \sum n \frac{n}{n + i} = n \to \infty lim \frac{1}{n} i = 1 \sum n \frac{1}{1 + ( \frac{i}{n} )} = \int_{0}^{1} \frac{1}{1 + x} d x

因此，

n \to \infty lim i = 1 \sum n j = 1 \sum n \frac{n}{( n + i ) ( n ^{2} + j ^{2} )} = n \to \infty lim (j = 1 \sum n \frac{n}{n ^{2} + j ^{2}}) (i = 1 \sum n \frac{n}{n + i}) = (n \to \infty lim j = 1 \sum n \frac{n}{n ^{2} + j ^{2}}) (n \to \infty lim i = 1 \sum n \frac{n}{n + i}) = (\int_{0}^{1} \frac{1}{1 + x} d x) (\int_{0}^{1} \frac{1}{1 + y ^{2}} d y) = \int_{0}^{1} d x \int_{0}^{1} \frac{1}{( 1 + x ) ( 1 + y ^{2} )} d y .

7

设向量组 $I : a_{1}, a_{2}, \dots, a_{r}$ 可由向量组 $II : β_{1}, β_{2}, \dots, β_{s}$ 线性表示，下列命题正确的是（　　）

正确答案：A

由于向量组 $I$ 能由向量组 $II$ 线性表示，所以 $r (I) \leq r (II)$ ，即

r (a_{1}, \dots, a_{r}) \leq r (β_{1}, \dots, β_{s}) \leq s

若向量组 $I$ 线性无关，则 $r (a_{1}, \dots, a_{r}) = r$ ，所以

r = r (a_{1}, \dots, a_{r}) \leq r (β_{1}, \dots, β_{s}) \leq s

即 $r \leq s$ ，选 (A)。

8

设 $A$ 为 4 阶实对称矩阵，且 $A^{2} + A = 0$ ，若 $A$ 的秩为 3，则 $A$ 相似于

正确答案：D

设 $λ$ 为 $A$ 的特征值。由于 $A^{2} + A = 0$ ，所以 $λ^{2} + λ = 0$ ，即 $λ (λ + 1) = 0$ 。因此 $A$ 的特征值只能为 $- 1$ 或 $0$ 。

由于 $A$ 为实对称矩阵，故 $A$ 可相似对角化，且相似对角矩阵中非零特征值的个数等于矩阵的秩。已知 $r (A) = 3$ ，所以 $A$ 有 3 个非零特征值，即 3 个 $- 1$ 和 1 个 $0$ 。

因此 $A$ 相似于

- 1 - 1 - 1 0

，选 (D)。

填空题

9

（填空题）3 阶常系数线性齐次微分方程 $y^{'''} - 2 y^{''} + y^{'} - 2 y = 0$ 的通解为 $y =$

10

（填空题）曲线 $y = \frac{2 x ^{3}}{x ^{2} + 1}$ 的斜渐近线方程为

11

（填空题）函数 $y = ln (1 - 2 x)$ 在 $x = 0$ 处的 $n$ 阶导数 $y^{(n)} (0) =$

12

（填空题）当 $0 \leq θ \leq π$ 时，对数螺线 $r = e^{θ}$ 的弧长为

13

（填空题）已知一个长方形的长 $l$ 以 $2 cm/s$ 的速率增加，宽 $w$ 以 $3 cm/s$ 的速率增加，则当 $l = 12 cm$ ， $w = 5 cm$ 时，它的对角线增加的速率为

14

（填空题）设 $A, B$ 为 3 阶矩阵，且 $∣ A ∣ = 3$ ， $∣ B ∣ = 2$ ， $∣ A^{- 1} + B ∣ = 2$ ，则 $∣ A + B^{- 1} ∣ =$

解答题

15

（本题满分 10 分）求函数 $f (x) = \int_{- \infty}^{x^{2}} (x^{2} - t) e^{- t^{2}} d t$ 的单调区间与极值。

16

（本题满分 10 分）

(I) 比较 $\int_{0}^{1} ∣ ln t ∣ [ln (1 + t)]^{n} d t$ 与 $\int_{0}^{1} ∣ ln t ∣ t^{n} d t$ $(n = 1, 2, \dots)$ 的大小，说明理由；

(II) 记 $u_{n} = \int_{0}^{1} ∣ ln t ∣ [ln (1 + t)]^{n} d t$ $(n = 1, 2, \dots)$ ，求极限 $lim_{n \to \infty} u_{n}$ 。

17

（本题满分 10 分）设 $y = f (x)$ 由参数方程

{x = 2 t + t^{2} y = ψ (t)

（ $t > - 1$ ）所确定， $ψ (1) = \frac{5}{2}$ ， $ψ^{'} (1) = 6$ ，已知 $\frac{d ^{2} y}{d x ^{2}} = \frac{3}{4 ( 1 + t )}$ ，求 $ψ (t)$ 。

18

（本题满分 10 分）一个高为 $l$ 的柱体形贮油罐，底面是长轴为 $2 a$ ，短轴为 $2 b$ 的椭圆。现将贮油罐平放，当油的高度为 $\frac{3}{2} b$ 时，计算油的质量（长度单位为 $m$ ，质量密度为常数 $ρ kg/ m^{3}$ ）。

19

（本题满分 10 分）设函数 $u = f (x, y)$ 具有二阶连续偏导数，且满足等式

4 \frac{\partial ^{2} u}{\partial x ^{2}} + 12 \frac{\partial ^{2} u}{\partial x \partial y} + 5 \frac{\partial ^{2} u}{\partial y ^{2}} = 0,

求 $a, b$ 的值，使等式在变换 $ξ = x + a y$ ， $η = x + b y$ 下化简为

\frac{\partial ^{2} u}{\partial ξ \partial η} = 0.

20

（本题满分 $11$ 分）计算二重积分 $I = \int_{D} r^{2} sin θ 1 - r^{2} cos 2 θ d r d θ$ ，其中 $D = {(r, θ) ∣ 0 \leq r \leq sec θ, 0 \leq θ \leq \frac{π}{4}}$ 。

21

（本题满分 11 分）

设函数 $f (x)$ 在闭区间 $[0, 1]$ 上连续，在开区间 $(0, 1)$ 内可导，且 $f (0) = 0$ ， $f (1) = \frac{1}{3}$ ．

证明：存在 $ξ \in (0, \frac{1}{2})$ ， $η \in (\frac{1}{2}, 1)$ ，使得：

f^{'} (ξ) + f^{'} (η) = ξ^{2} + η^{2} .

22

（本题满分 11 分）

(1) 已知矩阵 $A = λ 01 1 λ - 1 1 10 λ$ ，向量 $b = a 11$ ，若方程组 $A x = b$ 有两个不同的解，求 $λ$ ， $a$ ；

(2) 求方程组 $A x = b$ 的通解。

23

（本题满分 11 分）

设

A = 0 - 1 4 - 1 3 a 4 a 0

正交矩阵 $Q$ 使 $Q^{T} A Q$ 为对角矩阵，若 $Q$ 的第 1 列为 $\frac{1}{6} (1, 2, 1)^{T}$ ，求 $a$ ， $Q$ 。