2017 年真题

选择题

1

若函数 $f(x)=\begin{cases} \dfrac{1-\cos\sqrt{x}}{ax}, & x>0, \\ b, & x\leq0 \end{cases}$ 在 $x=0$ 处连续，则( )

高等数学函数、极限、连续函数的连续性

正确答案：A

【解】 $f(0+0)=\lim\limits_{x\to0^+}\dfrac{1-\cos\sqrt{x}}{ax}=\dfrac{1}{2a}$ ， $f(0)=f(0-0)=b$ ，

因为 $f(x)$ 在 $x=0$ 处连续，所以 $f(0+0)=f(0)=f(0-0)$ ，

从而 $ab=\dfrac{1}{2}$ ，应选(A).

2

设函数 $f(x)$ 可导，且 $f(x)f'(x)>0$ ，则（）

高等数学一元函数微分学导数的几何意义

正确答案：C

【解】方法一若 $f(x)>0$ ，则 $f'(x)>0$ ，从而 $f(1)>f(-1)>0$ ；

若 $f(x)<0$ ，则 $f'(x)<0$ ，从而 $f(1)\lt f(-1)<0$ ，

故 $|f(1)|>|f(-1)|$ ，应选（C）．

方法二由 $f(x)\cdot f'(x)=\left[\frac{1}{2}f^{2}(x)\right]'>0$ 得 $f^{2}(x)$ 单调递增，

从而 $f^{2}(1)>f^{2}(-1)$ ，故 $|f(1)|>|f(-1)|$ ，应选（C）．

3

函数 $f(x,y,z)=x^{2}y+z^{2}$ 在点 $(1,2,0)$ 处沿向量 $n=(1,2,2)$ 的方向导数为( )

高等数学多元函数微分学方向导数和梯度

正确答案：D

【解】 $\frac{\partial f}{\partial x}=2xy$ ， $\frac{\partial f}{\partial y}=x^{2}$ ， $\frac{\partial f}{\partial z}=2z$ ，

$\frac{\partial f}{\partial x}\big|_{(1,2,0)}=4$ ， $\frac{\partial f}{\partial y}\big|_{(1,2,0)}=1$ ， $\frac{\partial f}{\partial z}\big|_{(1,2,0)}=0$ ，

$\cos\alpha=\frac{1}{3}$ ， $\cos\beta=\frac{2}{3}$ ， $\cos\gamma=\frac{2}{3}$ ，

所求的方向导数为 $\frac{\partial f}{\partial \boxed{n}}\big|_{(1,2,0)}=4\times\frac{1}{3}+1\times\frac{2}{3}=2$ ，应选(D).

【答案】(D).

4

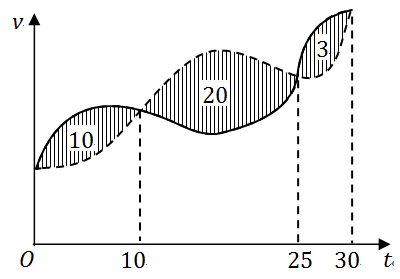
甲、乙两人赛跑，计时开始时，甲在乙前方 10（单位：m）处，图中，实线表示甲的速度曲线 $v = v_1(t)$ （单位：m/s），虚线表示乙的速度曲线 $v = v_2(t)$ ，三块阴影部分面积的数值依次是 10,20,3。计时开始后乙追上甲的时刻记为 $t_0$ （单位：s），则（）

高等数学一元函数积分学定积分的应用

正确答案：C

【解】
从 $t = 0$ 到 $t = t_0$ 的时间段内，甲、乙走过的距离分别为

S_1 = \int_{0}^{t_0} v_1(t) \, dt, \quad S_2 = \int_{0}^{t_0} v_2(t) \, dt.

在 $t = t_0$ 时，有 $S_1 = S_2 + 10$ ，即

\int_{0}^{t_0} v_1(t) \, dt = \int_{0}^{t_0} v_2(t) \, dt + 10,

或写作

\int_{0}^{t_0} \left[v_1(t) - v_2(t)\right] \, dt = 10.

由此解得 $t_0 = 25$ ，应选（C）。

5

设 $\alpha$ 为 $n$ 维单位列向量， $E$ 为 $n$ 阶单位矩阵，则（）

线性代数矩阵伴随矩阵与可逆矩阵

正确答案：A

【解】方法一 令 $A = αα^T$ ， $A^2 = A$ ，

令 $AX = λX$ ，由 $(A^2 - A)X = (λ^2 - λ)X = 0$ 得 $λ^2 - λ = 0$ ， $λ = 0$ 或 $λ = 1$ ，

因为 $tr A = α^Tα = 1 = λ_1 + \cdots + λ_n$ 得 $A$ 的特征值为 $λ_1 = \cdots = λ_{n - 1} = 0$ ， $λ_n = 1$ ，

$E - αα^T$ 的特征值为 $λ_1 = \cdots = λ_{n - 1} = 1$ ， $λ_n = 0$ ，从而 $|E - αα^T| = 0$ ，

即 $E - αα^T$ 不可逆，应选（A）.

方法二 令 $A = E - αα^T$ ， $A^2 = (E - αα^T)·(E - αα^T) = E - 2αα^T + αα^T = A$ ，

由 $A(E - A) = O$ 得 $r(A) + r(E - A) ≤ n$ ，

再由 $r(A) + r(E - A) ≥ r[A + (E - A)] = r(E) = n$ 得

$r(A) + r(E - A) = n$ ，

而 $E - A = αα^T$ ， $r(E - A) = r(αα^T) = r(α) = 1$ ，

于是 $r(A) = n - 1 < n$ ，即 $E - αα^T$ 不可逆，应选（A）.

6

已知矩阵 $A = \begin{pmatrix} 2&0&0 \\ 0&2&1 \\ 0&0&1 \end{pmatrix}$ , $B = \begin{pmatrix} 2&1&0 \\ 0&2&0 \\ 0&0&1 \end{pmatrix}$ , $C = \begin{pmatrix} 1&0&0 \\ 0&2&0 \\ 0&0&2 \end{pmatrix}$ , 则( )

线性代数矩阵的特征值与特征向量矩阵的相似与相似对角化

正确答案：B

【解】显然矩阵 $A,B,C$ 的特征值都是 $\lambda_1 = \lambda_2 = 2$ , $\lambda_3 = 1$ ,

由 $2E - A = \begin{pmatrix} 0&0&0 \\ 0&0&-1 \\ 0&0&1 \end{pmatrix}$ 得 $r(2E - A) = 1$ , 则 A 可相似对角化，从而 $A \sim C$ ;

由 $2E - B = \begin{pmatrix} 0&-1&0 \\ 0&0&0 \\ 0&0&1 \end{pmatrix}$

得 $r(2E - B) = 2$ , 则 $B$ 不可相似对角化，从而 $B$ 与 $A,C$ 不相似，

应选 (B)。

7

设 $A,B$ 为随机事件.若 $0<P(A)<1,0<P(B)<1$ ，则 $P(A|B)>P(A|\overline{B})$ 的充分必要条件是( )

概率论与数理统计随机事件和概率

正确答案：A

【解】由 $P(A|B)>P(A|\overline{B})$ 得 $\frac{P(AB)}{P(B)}>\frac{P(A\overline{B})}{P(\overline{B})}=\frac{P(A)-P(AB)}{1-P(B)}$ ，即

$P(A|B)>P(A|\overline{B})$ 等价于 $P(AB)>P(A)P(B)$ ；

由 $P(B|A)>P(B|\overline{A})$ 得 $\frac{P(AB)}{P(A)}>\frac{P(B)-P(AB)}{1-P(A)}$ ，即

$P(B|A)>P(B|\overline{A})$ 等价于 $P(AB)>P(A)P(B)$ ，应选(A)。

8

设 $X_{1},X_{2},\cdots,X_{n}(n\geq2)$ 为来自总体 $N(\mu,1)$ 的简单随机样本，记 $\overline{X}=\frac{1}{n}\sum_{i=1}^{n}X_{i}$ ，则下列结论中不正确的是（）

概率论与数理统计随机变量及其分布

正确答案：B

【解】若总体 $X\sim N(\mu,\sigma^{2})$ ，则

$\frac{1}{\sigma^{2}}\sum_{i=1}^{n}(X_{i}-\mu)^{2}\sim\chi^{2}(n)$ ， $\frac{1}{\sigma^{2}}\sum_{i=1}^{n}(X_{i}-\overline{X})^{2}\sim\chi^{2}(n - 1)$ ，

因为总体 $X\sim N(\mu,1)$ ，所以 $\sum_{i=1}^{n}(X_{i}-\mu)^{2}\sim\chi^{2}(n)$ ， $\sum_{i=1}^{n}(X_{i}-\overline{X})^{2}\sim\chi^{2}(n - 1)$ ，

再由 $\overline{X}\sim N(\mu,\frac{1}{n})$ 得 $\frac{\overline{X}-\mu}{\frac{1}{\sqrt{n}}}=\sqrt{n}(\overline{X}-\mu)\sim N(0,1)$ ，从而 $n(\overline{X}-\mu)^{2}\sim\chi^{2}(1)$ ，

不正确的是（B），应选（B）.

填空题

9

（填空题）已知函数 $f(x)=\frac{1}{1+x^2}$ ，则 $f^{(3)}(0)=$ ______．

高等数学一元函数微分学导数与微分的计算

【答案】 0

【解析】 方法一 $f(x)=\frac{1}{1+x^{2}} = 1 - x^{2} + x^{4} - x^{6} + x^{8} + o(x^{8})$ ，

由 $\frac{f^{(3)}(0)}{3!} = 0$ 得 $f^{(3)}(0) = 0$ 。

方法二根据求导改变奇偶性的性质，因为 $f(x)$ 为偶函数，所以 $f^{(3)}(x)$ 为奇函数，

故 $f^{(3)}(0) = 0$ 。

10

（填空题）微分方程 $y''+2y'+3y=0$ 的通解为 $y=$ ______．

高等数学常微分方程常系数齐次线性微分方程

【答案】 $\mathrm{e}^{-x}(C_{1}\cos\sqrt{2}x + C_{2}\sin\sqrt{2}x)$ （ $C_{1},C_{2}$ 为任意常数）

【解析】 【解】特征方程为 $\lambda^{2} + 2\lambda + 3 = 0$ ，特征值为 $\lambda_{1,2} = -1 \pm \sqrt{2}\mathrm{i}$ ，通解为 $y = \mathrm{e}^{-x}(C_{1}\cos\sqrt{2}x + C_{2}\sin\sqrt{2}x)$ （ $C_{1},C_{2}$ 为任意常数）

11

（填空题）若曲线积分 $\int_L \frac{xdx - aydy}{x^2 + y^2 - 1}$ 在区域 $D=\{(x,y)\mid x^2 + y^2 < 1\}$ 内与路径无关，则 $a=$ ______．

高等数学多元函数积分学第二类曲线积分

【答案】 -1

【解析】

P = \frac{x}{x^2 + y^2 - 1}, \quad Q = -\frac{ay}{x^2 + y^2 - 1}

\frac{\partial P}{\partial y} = -\frac{2xy}{(x^2 + y^2 - 1)^2}, \quad \frac{\partial Q}{\partial x} = \frac{2axy}{(x^2 + y^2 - 1)^2}

由于曲线积分与路径无关，

\frac{\partial Q}{\partial x} = \frac{\partial P}{\partial y}

代入得

\frac{2axy}{(x^2 + y^2 - 1)^2} = -\frac{2xy}{(x^2 + y^2 - 1)^2}

因此

a = -1

12

（填空题）幂级数 $\sum_{n=1}^{\infty} (-1)^{n-1}nx^{n-1}$ 在区间 $(-1,1)$ 内的和函数 $S(x)=$ ______．

高等数学无穷级数幂级数的和函数及幂级数展开式

【答案】 $\frac{1}{(1+x)^2}$

【解析】
方法一： $S(x)=\sum_{n=1}^{\infty}(-1)^{n-1}nx^{n-1} = -\left[\sum_{n=1}^{\infty}(-1)^nx^n\right]' = -\left(\frac{-x}{1+x}\right)' = \frac{1}{(1+x)^2}$

方法二：令 $S(x)=\sum_{n=1}^{\infty}(-1)^{n-1}nx^{n-1}$ ，

则 $\int_{0}^{x}S(x)\mathrm{d}x = \sum_{n=1}^{\infty}\int_{0}^{x}(-1)^{n-1}nx^{n-1}\mathrm{d}x = \sum_{n=1}^{\infty}(-1)^{n-1}x^n$

$= -\sum_{n=1}^{\infty}(-x)^n = -\frac{-x}{1+x} = \frac{x}{1+x}$ ，

故 $S(x)=\left(\frac{x}{1+x}\right)' = \frac{1}{(1+x)^2}$

13

（填空题）设矩阵 $A = \begin{pmatrix} 1 & 0 & 1 \\ 1 & 1 & 2 \\ 0 & 1 & 1 \end{pmatrix},$ $\boldsymbol{\alpha}_1, \boldsymbol{\alpha}_2, \boldsymbol{\alpha}_3$ 为线性无关的 $3$ 维列向量组，则向量组 $A\boldsymbol{\alpha}_1, A\boldsymbol{\alpha}_2, A\boldsymbol{\alpha}_3$ 的秩为______．

线性代数矩阵矩阵的秩

【答案】 2

【解析】
$(A\boldsymbol{\alpha}_{1}, A\boldsymbol{\alpha}_{2}, A\boldsymbol{\alpha}_{3}) = A(\boldsymbol{\alpha}_{1}, \boldsymbol{\alpha}_{2}, \boldsymbol{\alpha}_{3})$ 。

因为 $\boldsymbol{\alpha}_{1}, \boldsymbol{\alpha}_{2}, \boldsymbol{\alpha}_{3}$ 线性无关，所以 $(\boldsymbol{\alpha}_{1}, \boldsymbol{\alpha}_{2}, \boldsymbol{\alpha}_{3})$ 可逆，从而

r(A\boldsymbol{\alpha}_{1}, A\boldsymbol{\alpha}_{2}, A\boldsymbol{\alpha}_{3}) = r(A)

由

A \rightarrow \begin{pmatrix} 1 & 0 & 1 \\ 0 & 1 & 1 \\ 0 & 0 & 0 \end{pmatrix},

得 $r(A) = 2$ ，故向量组 $A\boldsymbol{\alpha}_{1}, A\boldsymbol{\alpha}_{2}, A\boldsymbol{\alpha}_{3}$ 的秩为 2。

14

（填空题）设随机变量 $X$ 的分布函数为 $F(x)=0.5\Phi(x)+0.5\Phi\left(\frac{x - 4}{2}\right)$ ，其中 $\Phi(x)$ 为标准正态分布函数，则 $E(X)=$ ______．

概率论与数理统计随机变量及其分布

【答案】 2

【解析】
随机变量 $X$ 的概率密度函数为

f(x) = 0.5\,\varphi(x) + 0.25\,\varphi\!\left( \frac{x - 4}{2} \right),

其数学期望为

\begin{aligned} E(X) &= \int_{-\infty}^{+\infty} x f(x) \, dx \\ &= 0.5 \int_{-\infty}^{+\infty} x \varphi(x) \, dx + 0.25 \int_{-\infty}^{+\infty} x \,\varphi\!\left( \frac{x - 4}{2} \right) dx \\ &= 0 + \int_{-\infty}^{+\infty} \left( \frac{x - 4}{2} + 2 \right) \varphi\!\left( \frac{x - 4}{2} \right) d\!\left( \frac{x - 4}{2} \right) \\ &= \int_{-\infty}^{+\infty} (t + 2) \varphi(t) \, dt \quad \left( \text{令 } t = \frac{x - 4}{2} \right) \\ &= 2 \int_{-\infty}^{+\infty} \varphi(t) \, dt \\ &= 2. \end{aligned}

解答题

15

（本题满分 10 分）

设函数 $f(u,v)$ 具有 2 阶连续偏导数， $y = f(\mathrm{e}^x, \cos x)$ ，求 $\frac{\mathrm{d}y}{\mathrm{d}x}\big|_{x = 0}$ ， $\frac{\mathrm{d}^2 y}{\mathrm{d}x^2}\big|_{x = 0}$ ．

高等数学多元函数微分学偏导数的概念与计算

【答案】
$\frac{\mathrm{d}y}{\mathrm{d}x}\big|_{x = 0} = f_1'(1,1)$
$\frac{\mathrm{d}^2 y}{\mathrm{d}x^2}\big|_{x = 0} = f_1'(1,1) + f_{11}''(1,1) - f_2'(1,1)$

【解析】

\frac{\mathrm{d}y}{\mathrm{d}x} = e^x f_1' - \sin x \cdot f_2', \quad \left. \frac{\mathrm{d}y}{\mathrm{d}x} \right|_{x = 0} = f_1'(1,1)

\begin{aligned} \frac{\mathrm{d}^2 y}{\mathrm{d}x^2} &= e^x f_1' + e^x \left( e^x f_{11}'' - \sin x \cdot f_{12}'' \right) \\ &\quad - \cos x \cdot f_2' - \sin x \left( e^x f_{21}'' - \sin x \cdot f_{22}'' \right) \end{aligned}

\left. \frac{\mathrm{d}^2 y}{\mathrm{d}x^2} \right|_{x = 0} = f_1'(1,1) + f_{11}''(1,1) - f_2'(1,1)

16

（本题满分 10 分）

\lim\limits_{n \to \infty} \sum\limits_{k=1}^{n} \frac{k}{n^2}\ln\left(1 + \frac{k}{n}\right) =

高等数学一元函数积分学定积分的概念、性质及几何意义

【答案】 $\frac{1}{4}$

【解析】

\begin{align*} &\lim_{n \to \infty} \sum_{k=1}^{n} \frac{k}{n^2} \ln\left(1 + \frac{k}{n}\right) \\ &= \lim_{n \to \infty} \frac{1}{n} \sum_{k=1}^{n} \frac{k}{n} \ln\left(1 + \frac{k}{n}\right) = \int_{0}^{1} x \ln(1 + x) \, dx \\ &= \frac{1}{2} \int_{0}^{1} \ln(1 + x) \, d(x^2) = \left[ \frac{1}{2} x^2 \ln(1 + x) \right]_{0}^{1} - \frac{1}{2} \int_{0}^{1} \frac{x^2}{1 + x} \, dx \\ &= \frac{1}{2} \ln 2 - \frac{1}{2} \int_{0}^{1} \left( x - 1 + \frac{1}{1 + x} \right) dx \\ &= \frac{1}{2} \ln 2 - \frac{1}{2} \left[ \frac{x^2}{2} - x + \ln(1 + x) \right]_{0}^{1} \\ &= \frac{1}{2} \ln 2 - \frac{1}{2} \left( \frac{1}{2} - 1 + \ln 2 \right) = \frac{1}{2} \ln 2 - \frac{1}{2} \left( \ln 2 - \frac{1}{2} \right) \\ &= \frac{1}{2} \ln 2 - \frac{1}{2} \ln 2 + \frac{1}{4} = \frac{1}{4} \end{align*}

17

（本题满分 10 分）

已知函数 $y(x)$ 由方程 $x^{3}+y^{3}-3x+3y-2 = 0$ 确定，求 $y(x)$ 的极值。

高等数学一元函数微分学函数的单调性、极值与最值

【答案】
极小值点为 $x=-1$ ， $y=0$ ；极大值点为 $x=1$ ， $y=1$ 。

【解析】
【解】 $x^{3}+y^{3}-3x+3y-2=0$ 两边对 $x$ 求导得 $3x^{2}+3y^{2}y'-3+3y'=0$ ，
令 $y'=0$ 得 $x_{1}=-1$ ， $x_{2}=1$ ，对应的函数值为 $y_{1}=0$ ， $y_{2}=1$ ；
$3x^{2}+3y^{2}y'-3+3y'=0$ 两边再对 $x$ 求导得 $6x+6yy'y''+3y^{2}y''+3y''=0$ ，
由 $y''(-1)=2>0$ 得 $x=-1$ 为极小值点，极小值为 $y=0$ ；
由 $y''(1)=-1<0$ 得 $x=1$ 为极大值点，极大值为 $y=1$ 。

18

（本题满分 10 分）

设函数 $f(x)$ 在区间 $[0,1]$ 上具有 2 阶导数，且 $f(1)>0,\lim\limits_{x \to 0^+}\frac{f(x)}{x}<0$ 证明：

(Ⅰ)方程 $f(x)=0$ 在区间 $(0,1)$ 内至少存在一个实根；

(Ⅱ)方程 $f(x)f''(x)+[f'(x)]^2=0$ 在区间 $(0,1)$ 内至少存在两个不同实根。

高等数学一元函数微分学方程根的存在性与个数

【答案】 见解析

【解析】
(Ⅰ) 根据极限的保号性，由于

\lim_{x \to 0^+} \frac{f(x)}{x} < 0,

存在 $\delta > 0$ ，使得当 $x \in (0, \delta)$ 时，

\frac{f(x)}{x} < 0,

即当 $x \in (0, \delta)$ 时， $f(x) < 0$ 。
于是存在 $c \in (0, \delta)$ ，满足 $f(c) < 0$ 。
又因为 $f(c) \cdot f(1) < 0$ ，由介值定理可知，存在 $x_0 \in (c, 1) \subset (0, 1)$ ，使得

f(x_0) = 0.

(Ⅱ) 令

F(x) = f(x) \cdot f'(x),

则

F'(x) = f(x) f''(x) + \left(f'(x)\right)^2.

由 $f(0) = f(c) = 0$ ，根据罗尔定理，存在 $\xi_1 \in (0, c)$ ，使得

f'(\xi_1) = 0.

由于 $f(0) = f(c) = 0$ ，可得

F(0) = F(\xi_1) = F(c) = 0.

再次应用罗尔定理，存在 $\eta_1 \in (0, \xi_1)$ 与 $\eta_2 \in (\xi_1, c)$ ，使得

F'(\eta_1) = 0, \quad F'(\eta_2) = 0,

即方程

f(x) f''(x) + \left(f'(x)\right)^2 = 0

在区间 $(0, 1)$ 内至少有两个不同的实根。

19

（本题满分 10 分）

设薄片型物体 $S$ 是圆锥面 $z = \sqrt{x^2 + y^2}$ 被柱面 $z^2 = 2x$ 割下的有限部分，其上任一点的密度为 $\mu(x, y, z) = 9\sqrt{x^2 + y^2 + z^2}$ 。记圆锥面与柱面的交线为 C。

(Ⅰ)求 $C$ 在 $xOy$ 平面上的投影曲线的方程；

(Ⅱ)求 $S$ 的质量 $M$ 。

高等数学多元函数积分学第一类曲面积分

【答案】
(Ⅰ) $C$ 在 $xOy$ 平面上的投影曲线的方程为 $\begin{cases} (x - 1)^2 + y^2 = 1 \\ z = 0 \end{cases}$ 。
(Ⅱ) $S$ 的质量 $M = 64$ 。

【解析】
（Ⅰ）由 $\begin{cases} z = \sqrt{x^2 + y^2} \\ z^2 = 2x \end{cases}$ ，得 $x^2 + y^2 = 2x$ ，
故 C 在 xOy 平面上的投影曲线为 $L:\begin{cases} (x - 1)^2 + y^2 = 1 \\ z = 0 \end{cases}$

（Ⅱ）

M = \iint_S 9\sqrt{x^2 + y^2 + z^2} \, dS

由

z_x' = \frac{x}{\sqrt{x^2 + y^2}}, \quad z_y' = \frac{y}{\sqrt{x^2 + y^2}}

得

dS = \sqrt{1 + z_x'^2 + z_y'^2} \, dxdy = \sqrt{2} \, dxdy

则

\begin{align*} M &= \iint_S 9\sqrt{x^2 + y^2 + z^2} \, dS \\ &= 9\sqrt{2} \iint_D \sqrt{x^2 + y^2} \cdot \sqrt{2} \, dx \, dy \\ &= 18 \iint_D \sqrt{x^2 + y^2} \, dx \, dy \\ &= 18 \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} d\theta \int_{0}^{2\cos\theta} r^2 \, dr \\ &= 18 \times \frac{8}{3} \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \cos^3\theta \, d\theta \\ &= 18 \times \frac{16}{3} \int_{0}^{\frac{\pi}{2}} \cos^3\theta \, d\theta \\ &= 64 \end{align*}

20

（本题满分 11 分）

设 3 阶矩阵 $A = (\alpha_1, \alpha_2, \alpha_3)$ 有 3 个不同的特征值，且 $\alpha_3 = \alpha_1 + 2\alpha_2$ 。

(Ⅰ) 证明 $r(A) = 2$ ；

(Ⅱ) 设 $\beta = \alpha_1 + \alpha_2 + \alpha_3$ ，求方程组 $Ax = \beta$ 的通解。

线性代数矩阵伴随矩阵与可逆矩阵

【答案】
(Ⅰ) 见解析
(Ⅱ) 方程组 $Ax = \beta$ 的通解为 $X = k\begin{pmatrix} 1 \\ 2 \\ -1 \end{pmatrix} + \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix}$ ，其中 $k$ 为任意常数。

【解析】
【证明】(Ⅰ)设 $A$ 的特征值为 $\lambda_1, \lambda_2, \lambda_3$ ，
因为 $A$ 有三个不同的特征值，所以 $A$ 可以相似对角化，即存在可逆矩阵 $P$ ，使得

P^{-1}AP = \begin{pmatrix} \lambda_1 & & \\ & \lambda_2 & \\ & & \lambda_3 \end{pmatrix}

因为 $\lambda_1, \lambda_2, \lambda_3$ 两两不同，所以 $r(A) \geq 2$ ，
又因为 $\alpha_3 = \alpha_1 + 2\alpha_2$ ，所以 $\alpha_1, \alpha_2, \alpha_3$ 线性相关，从而 $r(A) < 3$ ，于是 $r(A) = 2$ 。

(Ⅱ)因为 $r(A) = 2$ ，所以 $AX = 0$ 基础解系含一个线性无关的解向量，
由

\begin{cases} \alpha_1 + 2\alpha_2 - \alpha_3 = 0, \\ \alpha_1 + \alpha_2 + \alpha_3 = \beta, \end{cases}

得 $AX = \beta$ 的通解为

X = k\begin{pmatrix} 1 \\ 2 \\ -1 \end{pmatrix} + \begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} (k \text{})

21

（本题满分 11 分）

设二次型 $f(x_{1},x_{2},x_{3})=2x_{1}^{2}-x_{2}^{2}+ax_{3}^{2}+2x_{1}x_{2}-8x_{1}x_{3}+2x_{2}x_{3}$ 在正交变换 $\boldsymbol{x}=Q\boldsymbol{y}$ 下的标准形为 $\lambda_{1}y_{1}^{2}+\lambda_{2}y_{2}^{2}$ ，求 $a$ 的值及一个正交矩阵 $\boldsymbol{Q}$ ．

线性代数二次型

【答案】
a = 2，正交矩阵 $\boldsymbol{Q} = \begin{pmatrix} \frac{1}{\sqrt{3}} & -\frac{1}{\sqrt{2}} & \frac{1}{\sqrt{6}} \\ -\frac{1}{\sqrt{3}} & 0 & \frac{2}{\sqrt{6}} \\ \frac{1}{\sqrt{3}} & \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{6}} \end{pmatrix}$ ，标准形为 $-3y_1^2 + 6y_2^2$ 。

【解析】
【解】 $\boldsymbol{A}=\begin{pmatrix} 2&1&-4 \\ 1&-1&1 \\ -4&1&a \end{pmatrix}$ ， $\boldsymbol{X}=\begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix}$ ， $f(x_1,x_2,x_3)=\boldsymbol{X}^\text{T}\boldsymbol{A}\boldsymbol{X}$ ，

因为 $\lambda_3=0$ ，所以 $|\boldsymbol{A}|=0$ 。

由 $|\boldsymbol{A}|=\begin{vmatrix} 2&1&-4 \\ 1&-1&1 \\ -4&1&a \end{vmatrix}=-3(a - 2)=0$ ，得 $a = 2$ 。

由 $|\lambda\boldsymbol{E}-\boldsymbol{A}|=\begin{vmatrix} \lambda - 2&-1&4 \\ -1&\lambda + 1&-1 \\ 4&-1&\lambda - 2 \end{vmatrix}=\lambda(\lambda + 3)(\lambda - 6)= 0$ ，得 $\lambda_1 = -3$ ， $\lambda_2 = 6$ ， $\lambda_3 = 0$ ．

由 $-3\boldsymbol{E}-\boldsymbol{A}\to\begin{pmatrix} 5&1&-4 \\ 1&2&1 \\ -4&1&5 \end{pmatrix}\to\begin{pmatrix} 1&0&-1 \\ 0&1&1 \\ 0&0&0 \end{pmatrix}$

得 $\lambda_1 = -3$ 对应的线性无关的特征向量为 $\boldsymbol{\alpha}_1=\begin{pmatrix} 1 \\ -1 \\ 1 \end{pmatrix}$ ；

由 $6\boldsymbol{E}-\boldsymbol{A}=\begin{pmatrix} 4&-1&4 \\ -1&7&-1 \\ 4&-1&4 \end{pmatrix}\to\begin{pmatrix} 1&0&1 \\ 0&1&0 \\ 0&0&0 \end{pmatrix}$

得 $\lambda_2 = 6$ 对应的线性无关的特征向量为 $\boldsymbol{\alpha}_2=\begin{pmatrix} -1 \\ 0 \\ 1 \end{pmatrix}$ ；

由 $0\boldsymbol{E}-\boldsymbol{A}\to\begin{pmatrix} 1&0&-1 \\ 0&1&-2 \\ 0&0&0 \end{pmatrix}$ 得 $\lambda_3 = 0$ 对应的线性无关的特征向量为 $\boldsymbol{\alpha}_3=\begin{pmatrix} 1 \\ 2 \\ 1 \end{pmatrix}$ 。

规范化得 $\boldsymbol{\gamma}_1=\frac{1}{\sqrt{3}}\begin{pmatrix} 1 \\ -1 \\ 1 \end{pmatrix}$ ， $\boldsymbol{\gamma}_2=\frac{1}{\sqrt{2}}\begin{pmatrix} -1 \\ 0 \\ 1 \end{pmatrix}$ ， $\boldsymbol{\gamma}_3=\frac{1}{\sqrt{6}}\begin{pmatrix} 1 \\ 2 \\ 1 \end{pmatrix}$ ，故正交矩阵为 $\boldsymbol{Q}=\begin{pmatrix} \frac{1}{\sqrt{3}}&-\frac{1}{\sqrt{2}}&\frac{1}{\sqrt{6}} \\ -\frac{1}{\sqrt{3}}&0&\frac{2}{\sqrt{6}} \\ \frac{1}{\sqrt{3}}&\frac{1}{\sqrt{2}}&\frac{1}{\sqrt{6}} \end{pmatrix}$ ，

$f(x_1,x_2,x_3)=\boldsymbol{X}^\text{T}\boldsymbol{A}\boldsymbol{X}\stackrel{\boldsymbol{x}=\boldsymbol{Q}\boldsymbol{y}}{=}-3y_1^2 + 6y_2^2$ 。

22

（本题满分 11 分）

设随机变量 $X$ ， $Y$ 相互独立，且 $X$ 的概率分布为 $P\{X=0\} = P\{X=2\} = \frac{1}{2}$ ， $Y$ 的概率密度为

f(y) = \begin{cases} 2y, & 0 < y < 1, \\ 0, & \text{其他} \end{cases}

(Ⅰ) 求 $P\{Y \leq E(Y)\}$ ；

(Ⅱ) 求 $Z = X + Y$ 的概率密度。

概率论与数理统计随机变量的数字特征数学期望与方差

【答案】
(Ⅰ) $P\{Y \leq E(Y)\} = \frac{4}{9}$
(Ⅱ) $Z = X + Y$ 的概率密度为

f_Z(z) = \begin{cases} z, & 0 < z < 1, \\ z - 2, & 2 < z < 3, \\ 0, & \text{}. \end{cases}

【解析】
（Ⅰ）
$E(Y) = \int_{0}^{1} y \cdot 2y \, \text{d}y = \frac{2}{3}$ ，

P\{Y \leq E(Y)\} = P\left\{Y \leq \frac{2}{3}\right\} = \int_{0}^{\frac{2}{3}} 2y \, \text{d}y = \frac{4}{9}.

（Ⅱ）
方法一

F_Z(z) = P\{Z \leq z\} = P\{X + Y \leq z\}.

当 $z < 0$ 时， $F_Z(z) = 0$ ；
当 $z \geq 3$ 时， $F_Z(z) = 1$ ；
当 $0 \leq z < 1$ 时，
$F_Z(z) = P\{X = 0, Y \leq z\} = P\{X = 0\} P\{Y \leq z\} = \frac{1}{2} \int_{0}^{z} 2y \, \text{d}y = \frac{z^2}{2};$
当 $1 \leq z < 2$ 时，
$F_Z(z) = P\{X = 0, Y \leq z\} = P\{X = 0\} P\{Y \leq 1\} = \frac{1}{2};$
当 $2 \leq z < 3$ 时，
$F_Z(z) = P\{X = 0, Y \leq z\} + P\{X = 2, Y \leq z - 2\}$
$= P\{X = 0\} P\{Y \leq 1\} + P\{X = 2\} P\{Y \leq z - 2\}$
$= \frac{1}{2} + \frac{1}{2} \int_{0}^{z - 2} 2y \, \text{d}y = \frac{1}{2} + \frac{1}{2}(z - 2)^2.$

综上，

F_Z(z) = \begin{cases} 0, & z < 0, \\ \dfrac{z^2}{2}, & 0 \leq z < 1, \\ \dfrac{1}{2}, & 1 \leq z < 2, \\ \dfrac{1}{2} + \dfrac{1}{2}(z - 2)^2, & 2 \leq z < 3, \\ 1, & z \geq 3. \end{cases}

概率密度为

f_Z(z) = \begin{cases} z, & 0 < z < 1, \\ z - 2, & 2 < z < 3, \\ 0, & \text{}. \end{cases}

方法二
由全概率公式，

F_Z(z) = P\{Z \leq z\} = P\{X + Y \leq z\}

= P\{X = 0\} P\{X + Y \leq z \mid X = 0\} + P\{X = 2\} P\{X + Y \leq z \mid X = 2\}

= \frac{1}{2} P\{Y \leq z\} + \frac{1}{2} P\{Y \leq z - 2\}.

当 $z < 0$ 时， $F_Z(z) = 0$ ；
当 $0 \leq z < 1$ 时，
$F_Z(z) = \frac{1}{2} P\{Y \leq z\} = \frac{1}{2} \int_{0}^{z} 2y \, \text{d}y = \frac{z^2}{2};$
当 $1 \leq z < 2$ 时，
$F_Z(z) = \frac{1}{2} P\{Y \leq 1\} = \frac{1}{2};$
当 $2 \leq z < 3$ 时，
$F_Z(z) = \frac{1}{2} + \frac{1}{2} P\{Y \leq z - 2\} = \frac{1}{2} + \frac{1}{2} \int_{0}^{z - 2} 2y \, \text{d}y = \frac{1}{2} + \frac{(z - 2)^2}{2};$
当 $z \geq 3$ 时， $F_Z(z) = 1$ 。

故

f_Z(z) = F'(z) = \begin{cases} z, & 0 < z < 1, \\ z - 2, & 2 < z < 3, \\ 0, & \text{}. \end{cases}

23

（本题满分 11 分）

某工程师为了解一台天平的精度，用该天平对一物体的质量做 $n$ 次测量，该物体的质量 $\mu$ 是已知的。设 $n$ 次测量结果 $X_{1}, X_{2}, \cdots, X_{n}$ 相互独立且均服从正态分布 $N(\mu, \sigma^{2})$ ，该工程师记录的是 $n$ 次测量的绝对误差 $Z_{i} = |X_{i} - \mu| \ (i = 1, 2, \cdots, n)$ 。利用 $Z_{1}, Z_{2}, \cdots, Z_{n}$ 估计 $\sigma$ 。

(Ⅰ) 求 $Z_{1}$ 的概率密度；

(Ⅱ) 利用一阶矩求 $\sigma$ 的矩估计量；

(Ⅲ) 求 $\sigma$ 的最大似然估计量。

概率论与数理统计参数估计与假设检验矩估计和最大似然估计

【答案】
（Ⅰ） $Z_{1}$ 的概率密度为：

f(z) = \begin{cases} 0, & z \leq 0, \\ \frac{2}{\sigma} \varphi\left( \frac{z}{\sigma} \right), & z > 0, \end{cases}

其中 $\varphi(\cdot)$ 是标准正态分布的概率密度函数。

（Ⅱ） $\sigma$ 的矩估计量为：

\hat{\sigma} = \sqrt{\frac{\pi}{2}} \, \overline{Z}.

（Ⅲ） $\sigma$ 的最大似然估计量为：

\hat{\sigma} = \sqrt{\frac{1}{n} \sum_{i=1}^{n} Z_{i}^{2}}.

【解析】
【解】
（Ⅰ）由 $X_{1} \sim N(\mu, \sigma^{2})$ 得 $\frac{X_{1} - \mu}{\sigma} \sim N(0, 1)$ 。

$Z_{1}$ 的分布函数为 $F(z) = P\{ Z_{1} \leq z \}$ 。

当 $z < 0$ 时， $F(z) = 0$ ；

当 $z \geq 0$ 时，

F(z) = P\left\{ \left| \frac{X_{1} - \mu}{\sigma} \right| \leq \frac{z}{\sigma} \right\} = \Phi\left( \frac{z}{\sigma} \right) - \Phi\left( -\frac{z}{\sigma} \right) = 2\Phi\left( \frac{z}{\sigma} \right) - 1,

因此

F(z) = \begin{cases} 0, & z < 0, \\ 2\Phi\left( \frac{z}{\sigma} \right) - 1, & z \geq 0. \end{cases}

$Z_{1}$ 的密度函数为

f(z) = \begin{cases} 0, & z \leq 0, \\ \frac{2}{\sigma} \varphi\left( \frac{z}{\sigma} \right), & z > 0. \end{cases}

（Ⅱ）

E(Z) = E(|X_{i} - \mu|) = E(|X_{1} - \mu|)

= \int_{0}^{+\infty} z \cdot \frac{2}{\sigma} \varphi\left( \frac{z}{\sigma} \right) \, dz = 2\sigma \int_{0}^{+\infty} \frac{z}{\sigma} \varphi\left( \frac{z}{\sigma} \right) \, d\left( \frac{z}{\sigma} \right)

= 2\sigma \int_{0}^{+\infty} t \varphi(t) \, dt = \frac{2\sigma}{\sqrt{2\pi}} \int_{0}^{+\infty} t e^{-\frac{t^{2}}{2}} \, dt

= \frac{2\sigma}{\sqrt{2\pi}} \int_{0}^{+\infty} e^{-\frac{t^{2}}{2}} \, d\left( \frac{t^{2}}{2} \right) = \frac{2\sigma}{\sqrt{2\pi}}.

由 $\frac{2\sigma}{\sqrt{2\pi}} = \frac{1}{n} \sum_{i=1}^{n} Z_{i} = \overline{Z}$ ，得 $\sigma$ 的矩估计量为

\hat{\sigma} = \sqrt{\frac{\pi}{2}} \, \overline{Z}.

（Ⅲ）似然函数为

L = f(z_{1}) \cdots f(z_{n}) = \frac{2^{n}}{\sigma^{n}} \cdot \left( \frac{1}{\sqrt{2\pi}} \right)^{n} \cdot e^{-\frac{1}{2\sigma^{2}} (z_{1}^{2} + \cdots + z_{n}^{2})} \quad (z_{i} > 0, i = 1, 2, \dots, n),

\ln L = n \ln 2 - n \ln \sigma - n \ln \sqrt{2\pi} - \frac{1}{2\sigma^{2}} (z_{1}^{2} + \cdots + z_{n}^{2}).

由

\frac{d \ln L}{d \sigma} = -\frac{n}{\sigma} + \frac{1}{\sigma^{3}} (z_{1}^{2} + \cdots + z_{n}^{2}) = 0

得

\hat{\sigma} = \sqrt{\frac{1}{n} \sum_{i=1}^{n} z_{i}^{2}},

故 $\sigma$ 的最大似然估计量为

\hat{\sigma} = \sqrt{\frac{1}{n} \sum_{i=1}^{n} Z_{i}^{2}}.