2015 年真题

选择题

1

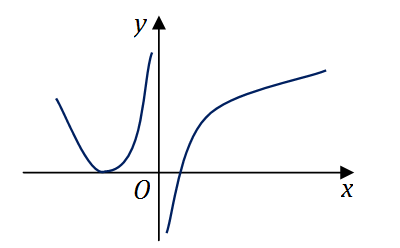
设函数 $f(x)$ 在 $(-\infty, +\infty)$ 上连续，其二阶导数 $f''(x)$ 的图形如右图所示，则曲线 $y = f(x)$ 在 $(-\infty, +\infty)$ 的拐点个数为

高等数学一元函数微分学曲线的凹凸性、拐点及渐近线

正确答案：C

对于连续函数的曲线而言，拐点处的二阶导数等于零或者不存在。

从图上可以看出有两个二阶导数等于零的点，以及一个二阶导数不存在的点 $x=0$ 。

对于这三个点，左边二阶导数等于零的点的两侧，二阶导数都是正的，因此对应的点不是拐点。

而另外两个点的两侧，二阶导数是异号的，对应的点才是拐点。

所以应该选 (C)。

2

设 $y = \frac{1}{2} e^{2x} + \left( x - \frac{1}{3} \right) e^{x}$ 是二阶常系数非齐次线性微分方程 $y^{\prime\prime} + a y' + b y = c e^{x}$ 的一个特解，则

高等数学常微分方程常系数非齐次线性微分方程

正确答案：A

线性微分方程的特征方程为 $r^{2} + a r + b = 0$ ，由特解可知 $r_{1} = 2$ 一定是特征方程的一个实根。

如果 $r_{2} = 1$ 不是特征方程的实根，则对应于 $f(x) = c e^{x}$ 的特解形式应为 $Q(x) e^{x}$ ，其中 $Q(x)$ 应是一个零次多项式，即常数，这与条件不符。

因此， $r_{2} = 1$ 也是特征方程的另一个实根。由韦达定理可得：

a = -(2 + 1) = -3, \quad b = 2 \times 1 = 2.

同时， $y^{*} = x e^{x}$ 是原方程的一个解，代入可得 $c = -1$ ，应选 (A)。

3

若级数 $\sum_{n=1}^{\infty} a_{n}$ 条件收敛，则 $x = \sqrt{3}$ 与 $x = 3$ 对于幂级数 $\sum_{n=1}^{\infty} n a_{n} (x - 1)^{n}$ 的

高等数学无穷级数求幂级数的收敛半径、收敛区间和收敛域

正确答案：B

设幂级数 $\sum_{n=1}^{\infty} a_{n}$ 条件收敛，表明幂级数 $\sum_{n=1}^{\infty} a_{n} x^{n}$ 在 $x = 1$ 处条件收敛，即该幂级数的收敛半径为 $1$ ，故有：

\lim_{n \to \infty} \left| \frac{a_{n+1}}{a_{n}} \right| = 1.

因此，对于幂级数 $\sum_{n=1}^{\infty} n a_{n} (x - 1)^{n}$ ，其收敛半径为：

R = \lim_{n \to \infty} \left| \frac{n a_{n}}{(n+1) a_{n+1}} \right| = 1,

收敛区间为 $(0, 2)$ 。

显然， $x = \sqrt{3}$ 位于收敛区间内，为收敛点；而 $x = 3$ 不在收敛区间内，为发散点。

因此，应选 (B)。

4

设 $D$ 是第一象限中由曲线 $2xy = 1$ ， $4xy = 1$ 与直线 $y = x$ ， $y = \sqrt{3}x$ 所围成的平面区域，函数 $f(x, y)$ 在 $D$ 上连续，则

\iint_{D} f(x, y) \, dx \, dy

化为极坐标下的二次积分是

高等数学多元函数积分学交换积分次序与坐标系之间的转化

\int_{\frac{\pi}{4}}^{\frac{\pi}{3}} d \theta \int_{\frac{1}{\sqrt{2 \sin 2 \theta}}}^{\frac{1}{\sqrt{\sin 2 \theta}}} f(r \cos \theta, r \sin \theta) r d r

\int_{\frac{\pi}{4}}^{\frac{\pi}{3}} d \theta \int_{\frac{1}{\sqrt{\sin 2 \theta}}}^{\frac{1}{\sqrt{2 \sin 2 \theta}}} f(r \cos \theta, r \sin \theta) r d r

\int_{\frac{\pi}{4}}^{\frac{\pi}{3}} d \theta \int_{\frac{1}{\sqrt{2 \sin \theta}}}^{\frac{1}{\sqrt{\sin \theta}}} f(r \cos \theta, r \sin \theta) d r

\int_{\frac{\pi}{4}}^{\frac{\pi}{3}} d \theta \int_{\frac{1}{\sqrt{\sin \theta}}}^{\frac{1}{\sqrt{2 \sin \theta}}} f(r \cos \theta, r \sin \theta) d r

正确答案：A

积分区域如图所示，化成极坐标方程：

曲线 $2xy = 1$ 化为 $r^{2} \sin 2\theta = 1$ ，即 $r = \frac{1}{\sqrt{2 \sin 2\theta}}$ 。

曲线 $4xy = 1$ 化为 $r^{2} \sin 2\theta = \frac{1}{2}$ ，即 $r = \frac{1}{\sqrt{\sin 2\theta}}$ 。

直线 $y = x$ 对应 $\theta = \frac{\pi}{4}$ ，直线 $y = \sqrt{3}x$ 对应 $\theta = \frac{\pi}{3}$ 。

因此，积分表达式为：

\iint_{D} f(x, y) \, dx \, dy = \int_{\frac{\pi}{4}}^{\frac{\pi}{3}} d\theta \int_{\frac{1}{\sqrt{2 \sin 2\theta}}}^{\frac{1}{\sqrt{\sin 2\theta}}} f(r \cos \theta, r \sin \theta) \, r \, dr

应该选 (A)。

5

设矩阵 $\boldsymbol{A} = \begin{pmatrix} 1 & 1 & 1 \\ 1 & 2 & a \\ 1 & 4 & a^2 \end{pmatrix}$ ， $\boldsymbol{b} = \begin{pmatrix} 1 \\ d \\ d^2 \end{pmatrix}$ ，若集合 $\Omega = \{1, 2\}$ ，则线性方程组 $\boldsymbol{A}\boldsymbol{x} = \boldsymbol{b}$ 有无穷多解的充分必要条件是

线性代数线性方程组

正确答案：D

对线性方程组的增广矩阵进行初等行变换：方程组有无穷多解的充分必要条件是 $r(A) = r(A, b) < 3$ ，即

(a - 1)(a - 2) = 0 \quad \text{且} \quad (d - 1)(d - 2) = 0

同时成立。因此，应选 (D)。

6

设二次型 $f(x_{1}, x_{2}, x_{3})$ 在正交变换 $x = P y$ 下的标准形为 $2 y_{1}^{2} + y_{2}^{2} - y_{3}^{2}$ ，其中 $P = (e_{1}, e_{2}, e_{3})$ ，若 $Q = (e_{1}, -e_{3}, e_{2})$ ，则 $f(x_{1}, x_{2}, x_{3})$ 在 $x = Q y$ 下的标准形为

线性代数二次型

正确答案：A

设 $Q = (e_1, -e_3, e_2) = (e_1, e_2, e_3) \begin{pmatrix} 1 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & -1 & 0 \end{pmatrix} = P \begin{pmatrix} 1 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & -1 & 0 \end{pmatrix}$ ，则 $Q^T = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 0 & -1 \\ 0 & 1 & 0 \end{pmatrix} P^T$ 。

已知 $f = x^T A x = y^T P^T A P y = y^T \begin{pmatrix} 2 & & \\ & 1 & \\ & & -1 \end{pmatrix} y$ ，因此：

\begin{align*} Q^T A Q &= \begin{pmatrix} 1 & 0 & 0 \\ 0 & 0 & -1 \\ 0 & 1 & 0 \end{pmatrix} P^T A P \begin{pmatrix} 1 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & -1 & 0 \end{pmatrix} \\ &= \begin{pmatrix} 1 & 0 & 0 \\ 0 & 0 & -1 \\ 0 & 1 & 0 \end{pmatrix} \begin{pmatrix} 2 & & \\ & 1 & \\ & & -1 \end{pmatrix} \begin{pmatrix} 1 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & -1 & 0 \end{pmatrix} \\ &= \begin{pmatrix} 2 & & \\ & -1 & \\ & & 1 \end{pmatrix}. \end{align*}

故选择 (A)。

7

若 $A$ ， $B$ 为任意两个随机事件，则

概率论与数理统计随机事件和概率

正确答案：C

因为 $P(A) \geq P(AB)$ 且 $P(B) \geq P(AB)$ ，所以 $2P(AB) \leq P(A) + P(B)$ ，即 $P(AB) \leq \frac{P(A) + P(B)}{2}$ 。

快速选 (C)。

8

设随机变量 $X$ 、 $Y$ 不相关，且 $E X = 2$ ， $E Y = 1$ ， $D X = 3$ ，则 $E(X(X + Y - 2)) = ( \quad )$ 。

概率论与数理统计随机变量的数字特征数学期望与方差

正确答案：D

首先，计算期望 $E(X(X+Y-2))$ ：

E(X(X+Y-2)) = E(X^2) + E(XY) - 2E(X)

接着，利用方差与期望的关系 $D(X) = E(X^2) - (E(X))^2$ ，代入 $E(X^2) = D(X) + (E(X))^2$ ：

E(X(X+Y-2)) = D(X) + (E(X))^2 + E(XY) - 2E(X)

由于 $X$ 与 $Y$ 相互独立，有 $E(XY) = E(X)E(Y)$ ，代入已知数值 $D(X) = 3$ ， $E(X) = 2$ ， $E(Y) = 1$ ：

E(X(X+Y-2)) = 3 + 2^2 + 2 \times 1 - 2 \times 2

计算得：

3 + 4 + 2 - 4 = 5

因此，答案为 $5$ ，应选择 (D)。

填空题

9

（填空题） $\lim\limits_{x \to 0} \frac{\ln(\cos x)}{x^2} =$ ______

高等数学函数、极限、连续函数极限的计算

【答案】 $-\frac{1}{2}$

【解析】
$\lim_{x \to 0} \frac{\ln (\cos x)}{x^{2}} = \lim_{x \to 0} \frac{-\tan x}{2x} = -\frac{1}{2}$

10

（填空题） $\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\left( \frac{\sin x}{1 + \cos x}+\vert x\vert\right)\mathrm{d}x =$ ______.

高等数学一元函数积分学定积分的计算

【答案】 $\frac{\pi^{2}}{4}$

【解析】 只要注意 $\frac{\sin x}{1+\cos x}$ 为奇函数，在对称区间上积分为零。

所以 $\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\left(\frac{\sin x}{1+\cos x}+|x|\right) dx = 2 \int_{0}^{\frac{\pi}{2}} x dx = \frac{\pi^{2}}{4}$

11

（填空题）若函数 $z=z(x, y)$ 是由方程 $e^{z}+xyz+x+\cos x=2$ 确定，则 $dz|_{(0,1)}=$

高等数学多元函数微分学全微分的概念与计算

【答案】 $-dx$

【解析】

我们已知函数

F(x, y, z) = e^{z} + x y z + x + \cos x - 2

其偏导数为：

F^\prime_{x}(x, y, z) = y z + 1 - \sin x, \quad F^\prime_{y}(x, y, z) = x z, \quad F^\prime_{z}(x, y, z) = e^{z} + x y

在点 $(x, y, z) = (0, 1, 0)$ 处，有：

F^\prime_{x}(0, 1, 0) = 1 \cdot 0 + 1 - \sin 0 = 1, \quad F^\prime_{y}(0, 1, 0) = 0, \quad F^\prime_{z}(0, 1, 0) = e^{0} + 0 \cdot 1 = 1

由隐函数求导公式：

\left.\frac{\partial z}{\partial x}\right|_{(0,1)} = -\frac{F_x(0,1,0)}{F_z(0,1,0)} = -1,\quad

\left.\frac{\partial z}{\partial y}\right|_{(0,1)} = -\frac{F_y(0,1,0)}{F_z(0,1,0)} = 0

因此，

\left. dz \right|_{(0,1)} = -1 \cdot dx + 0 \cdot dy = -dx

12

（填空题）设 $\Omega$ 是由平面 $x + y + z = 1$ 和三个坐标面围成的空间区域，则

\iiint_{\Omega} (x + 2y + 3z) \, dx \, dy \, dz =

高等数学多元函数积分学重积分的计算

【答案】 $\frac{1}{4}$

【解析】 【详解】注意在积分区域内，三个变量 $x$ 、 $y$ 、 $z$ 具有轮换对称性，即

\iiint_{\Omega} x \, dx \, dy \, dz = \iiint_{\Omega} y \, dx \, dy \, dz = \iiint_{\Omega} z \, dx \, dy \, dz

因此，

\iiint_{\Omega} (x + 2y + 3z) \, dx \, dy \, dz = 6 \iiint_{\Omega} z \, dx \, dy \, dz

进一步计算：

6 \iiint_{\Omega} z \, dx \, dy \, dz = 6 \int_{0}^{1} z \, dz \iint_{D_z} dx \, dy

其中， $D_z$ 为 $z$ 固定时的截面区域，面积为 $(1 - z)^2$ ，于是

6 \int_{0}^{1} z (1 - z)^2 \, dz = 3 \int_{0}^{1} z (1 - z)^2 \, dz

计算该积分：

\begin{align*} 3 \int_{0}^{1} z (1 - z)^2 \, dz &= 3 \int_{0}^{1} (z - 2z^2 + z^3) \, dz \\ &= 3 \left[ \frac{z^2}{2} - \frac{2z^3}{3} + \frac{z^4}{4} \right]_{0}^{1} \\ &= 3 \left( \frac{1}{2} - \frac{2}{3} + \frac{1}{4} \right) \\ &= \frac{1}{4} \end{align*}

最终结果为 $\frac{1}{4}$ 。

13

（填空题） $n$ 阶行列式 $\left|\begin{array}{ccccc} 2 & 0 & \cdots & 0 & 2 \\ -1 & 2 & \cdots & 0 & 2 \\ \vdots & \ddots & \ddots & \vdots & \vdots \\ 0 & 0 & \cdots & 2 & 2 \\ 0 & 0 & \cdots & -1 & 2 \end{array}\right| =$

线性代数行列式

【答案】

D_n = 2^{n+1} - 2

【解析】 按照第一行展开，得

D_n = 2 D_{n-1} + (-1)^{n+1} \cdot 2(-1)^{n-1} = 2 D_{n-1} + 2,

于是有

D_n + 2 = 2(D_{n-1} + 2).

已知 $D_1 = 2$ ， $D_2 = 6$ ，可得

D_n = 2^{n+1} - 2.

14

（填空题）设二维随机变量 $(X, Y)$ 服从正态分布 $N(1, 0; 1, 1; 0)$ ，则 $P\{X Y - Y < 0\} =$

概率论与数理统计多维随机变量及其分布二维随机变量及其分布

【答案】 $\frac{1}{2}$

【解析】 【详解】由于相关系数等于零，所以 $X$ 、 $Y$ 都服从正态分布， $X \sim N(1,1)$ ， $Y \sim N(0,1)$ ，且相互独立。因此， $X-1 \sim N(0,1)$ 。

P\{XY - Y < 0\} = P\{Y(X-1) < 0\}

由于 $Y$ 与 $X-1$ 相互独立，且均服从标准正态分布，可得：

P\{Y(X-1) < 0\} = P\{Y < 0, X-1 > 0\} + P\{Y > 0, X-1 < 0\}

= \frac{1}{2} \times \frac{1}{2} + \frac{1}{2} \times \frac{1}{2} = \frac{1}{4} + \frac{1}{4} = \frac{1}{2}

解答题

15

（本题满分 10 分）设函数 $f(x) = x + a \ln (1 + x) + b x \sin x$ ， $g(x) = k x^{3}$ 在 $x \to 0$ 时为等价无穷小，求常数 $a, b, k$ 的取值。

高等数学函数、极限、连续确定极限中的参数

【答案】 $a = -1$ ， $b = -\frac{1}{2}$ ， $k = -\frac{1}{3}$

【解析】 设函数 $f(x) = x + a \ln (1+x) + b x \sin x$ 与 $g(x) = k x^3$ 在 $x \to 0$ 时为等价无穷小，即：

\lim_{x \to 0} \frac{f(x)}{g(x)} = 1

代入 $f(x)$ 和 $g(x)$ ：

\lim_{x \to 0} \frac{x + a \ln (1+x) + b x \sin x}{k x^3} = 1

等价于：

\lim_{x \to 0} \frac{x + a \ln (1+x) + b x \sin x}{x^3} = k

为确保极限存在，需使分子在 $x=0$ 处的低阶项为零。首先计算 $f(0)$ ：

f(0) = 0 + a \ln 1 + b \cdot 0 \cdot \sin 0 = 0

计算一阶导数 $f'(x)$ ：

f'(x) = 1 + a \cdot \frac{1}{1+x} + b (\sin x + x \cos x)

在 $x=0$ 处：

f'(0) = 1 + a \cdot 1 + b \cdot 0 = 1 + a

为使 $f(x)$ 是比 $x$ 更高阶的无穷小，需 $f'(0) = 0$ ，即：

1 + a = 0 \implies a = -1

代入 $a = -1$ ，得：

f(x) = x - \ln (1+x) + b x \sin x

计算二阶导数 $f''(x)$ ：

f'(x) = 1 - \frac{1}{1+x} + b \sin x + b x \cos x

f''(x) = \frac{1}{(1+x)^2} + b \cos x + b \cos x - b x \sin x = \frac{1}{(1+x)^2} + 2b \cos x - b x \sin x

在 $x=0$ 处：

f''(0) = \frac{1}{1} + 2b \cdot 1 - 0 = 1 + 2b

为使 $f(x)$ 是比 $x^2$ 更高阶的无穷小，需 $f''(0) = 0$ ，即：

1 + 2b = 0 \implies b = -\frac{1}{2}

代入 $b = -\frac{1}{2}$ ，得：

f(x) = x - \ln (1+x) - \frac{1}{2} x \sin x

现在求极限：

\lim_{x \to 0} \frac{f(x)}{x^3} = \lim_{x \to 0} \frac{x - \ln (1+x) - \frac{1}{2} x \sin x}{x^3}

使用泰勒展开： $\ln (1+x) = x - \frac{x^2}{2} + \frac{x^3}{3} - O(x^4)$ ， $\sin x = x - \frac{x^3}{6} + O(x^5)$ ，代入：

x - \ln (1+x) = x - \left( x - \frac{x^2}{2} + \frac{x^3}{3} - O(x^4) \right) = \frac{x^2}{2} - \frac{x^3}{3} + O(x^4)

-\frac{1}{2} x \sin x = -\frac{1}{2} x \left( x - \frac{x^3}{6} + O(x^5) \right) = -\frac{1}{2} x^2 + \frac{1}{12} x^4 + O(x^6)

相加：

f(x) = \left( \frac{x^2}{2} - \frac{x^3}{3} \right) + \left( -\frac{1}{2} x^2 \right) + O(x^4) = -\frac{x^3}{3} + O(x^4)

因此：

\lim_{x \to 0} \frac{f(x)}{x^3} = \lim_{x \to 0} \frac{-\frac{x^3}{3} + O(x^4)}{x^3} = -\frac{1}{3}

故 $k = -\frac{1}{3}$ 。

验证：

\lim_{x \to 0} \frac{f(x)}{g(x)} = \lim_{x \to 0} \frac{f(x)}{k x^3} = \lim_{x \to 0} \frac{f(x)}{-\frac{1}{3} x^3} = \frac{\lim_{x \to 0} \frac{f(x)}{x^3}}{-\frac{1}{3}} = \frac{-\frac{1}{3}}{-\frac{1}{3}} = 1

满足等价无穷小条件。

因此，常数取值为 $a = -1$ ， $b = -\frac{1}{2}$ ， $k = -\frac{1}{3}$ 。

16

（本题满分 10 分）设函数 $y = f(x)$ 在定义域 $I$ 上的导数大于零，若对任意的 $x_0 \in I$ ，曲线 $y = f(x)$ 在点 $(x_0, f(x_0))$ 处的切线与直线 $x = x_0$ 及 $x$ 轴所围成区域的面积恒为 4，且 $f(0) = 2$ ，求 $f(x)$ 的表达式。

高等数学一元函数积分学定积分的应用

【答案】 $y = \frac{8}{4 - x}$

【解析】 函数 $y = f(x)$ 在点 $(x_0, f(x_0))$ 处的切线方程为

y = f'(x_0)(x - x_0) + f(x_0)

令 $y = 0$ ，解得

x = x_0 - \frac{f(x_0)}{f'(x_0)}

曲线在该点处的切线与直线 $x = x_0$ 及 $x$ 轴所围成区域的面积为

S = \frac{1}{2} f(x_0) \left| x_0 - \left( x_0 - \frac{f(x_0)}{f'(x_0)} \right) \right| = 4

整理得

\frac{f^2(x_0)}{2 f'(x_0)} = 4

即

f'(x) = \frac{1}{8} f^2(x)

分离变量得

\frac{1}{f(x)} = C - \frac{1}{8} x

由 $f(0) = 2$ 得 $C = \frac{1}{2}$ ，所求函数表达式为

y = \frac{8}{4 - x}

17

（本题满分 10 分）设函数 $f(x, y)=x+y+xy$ ，曲线 $C: x^{2}+y^{2}+xy=3$ ，求 $f(x, y)$ 在曲线 $C$ 上的最大方向导数。

高等数学多元函数微分学方向导数和梯度

【答案】 最大方向导数为 3

【解析】 函数 $f(x, y)=x+y+xy$ 在 $(x, y)$ 处的梯度为 $\text{grad}f=(1+y, 1+x)$ ，其模为 $|\text{grad}f|=\sqrt{(1+y)^{2}+(1+x)^{2}}$ ，此问题转化为求函数 $F(x, y)=(1+x)^{2}+(1+y)^{2}$ 在条件 $C: x^{2}+y^{2}+xy=3$ 下的条件极值。用拉格朗日乘子法，令 $L(x, y, \lambda)=(1+x)^{2}+(1+y)^{2}+\lambda(x^{2}+y^{2}+xy-3)$ ，解方程组

\begin{cases} L_{x}'=2(1+x)+(2x + y)\lambda=0 \\ L_{y}'=2(1+y)+(2y + x)\lambda=0 \\ x^{2}+y^{2}+xy=3 \end{cases}

可得在点 $(2, -1)$ 或 $(-1, 2)$ 处方向导数取到最大，最大值为 $\sqrt{9}=3$ 。

18

（本题满分 10 分）

(1) 设函数 $u(x)$ ， $v(x)$ 都可导，利用导数定义证明 $(u(x)v(x))' = u'(x)v(x) + u(x)v'(x)$ ；

(2) 设函数 $u_{1}(x)$ ， $u_{2}(x)$ ， $\cdots$ ， $u_{n}(x)$ 都可导， $f(x) = u_{1}(x)u_{2}(x)\cdots u_{n}(x)$ ，写出 $f(x)$ 的求导公式。

高等数学一元函数微分学导数与微分的计算

【答案】
(1) 见解析
(2)

f'(x) = u_{1}'(x)u_{2}(x) \cdots u_{n}(x) + u_{1}(x)u_{2}'(x) \cdots u_{n}(x) + \cdots + u_{1}(x)u_{2}(x) \cdots u_{n}'(x)

【解析】
(1) 证明：设 $y = u(x)v(x)$ ，则

\begin{align*} \Delta y &= u(x + \Delta x)v(x + \Delta x) - u(x)v(x) \\ &= u(x + \Delta x)v(x + \Delta x) - u(x)v(x + \Delta x) \\ &\quad + u(x)v(x + \Delta x) - u(x)v(x) \\ &= \Delta u \cdot v(x + \Delta x) + u(x) \cdot \Delta v, \end{align*}

所以

\frac{\Delta y}{\Delta x} = \frac{\Delta u}{\Delta x} \cdot v(x + \Delta x) + u(x) \cdot \frac{\Delta v}{\Delta x}.

由导数的定义和可导与连续的关系，得

y' = \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} = u'(x)v(x) + u(x)v'(x).

(2) 设 $f(x) = u_{1}(x)u_{2}(x)\cdots u_{n}(x)$ ，其求导公式为

f'(x) = u_{1}'(x)u_{2}(x) \cdots u_{n}(x) + u_{1}(x)u_{2}'(x) \cdots u_{n}(x) + \cdots + u_{1}(x)u_{2}(x) \cdots u_{n}'(x).

19

（本题满分10分）已知曲线 $L$ 的方程为

\begin{cases} z = \sqrt{2 - x^2 - y^2} \\ z = x \end{cases}

起点为 $A(0, \sqrt{2}, 0)$ ，终点为 $B(0, -\sqrt{2}, 0)$ ，计算曲线积分

\int_{L}(y + z)dx + (z^2 - x^2 + y)dy + (x^2 + y^2)dz

高等数学多元函数积分学第二类曲线积分

【答案】 $\frac{\sqrt{2}}{2} \pi$

【解析】 曲线 $L$ 的参数方程为

\begin{cases} x = \cos t \\ y = \sqrt{2} \sin t \\ z = \cos t \end{cases}

起点 $A(0, \sqrt{2}, 0)$ 对应 $t = \frac{\pi}{2}$ ，终点为 $B(0, -\sqrt{2}, 0)$ 对应 $t = -\frac{\pi}{2}$ 。

\int_{L} (y + z) \, dx + (z^2 - x^2 + y) \, dy + (x^2 + y^2) \, dz

= \int_{\frac{\pi}{2}}^{-\frac{\pi}{2}} (\sqrt{2} \sin t + \cos t) \, d(\cos t) + (\sqrt{2} \cos t) \, d(\sqrt{2} \cos t) + (2 - \cos^2 t) \, d\cos t

= 2\sqrt{2} \int_{0}^{\frac{\pi}{2}} \sin^2 t \, dt = \frac{\sqrt{2}}{2} \pi

20

（本题满分 11 分）设向量组 $\alpha_{1}$ ， $\alpha_{2}$ ， $\alpha_{3}$ 为向量空间 $\mathbb{R}^{3}$ 的一组基， $\beta_{1} = 2\alpha_{1} + 2k\alpha_{3}$ ， $\beta_{2} = 2\alpha_{2}$ ， $\beta_{3} = \alpha_{1} + (k+1)\alpha_{3}$ 。

(1) 证明：向量组 $\beta_{1}$ ， $\beta_{2}$ ， $\beta_{3}$ 为向量空间 $\mathbb{R}^{3}$ 的一组基；

(2) 当 $k$ 为何值时，存在非零向量 $\xi$ ，使得 $\xi$ 在基 $\alpha_{1}$ ， $\alpha_{2}$ ， $\alpha_{3}$ 和基 $\beta_{1}$ ， $\beta_{2}$ ， $\beta_{3}$ 下的坐标相同，并求出所有的非零向量。

线性代数向量向量组的线性相关性

【答案】
(1) 见解析
(2) 当 $k=0$ 时，存在非零向量 $\xi$ ，使得 $\xi$ 在基 $\alpha_{1}$ ， $\alpha_{2}$ ， $\alpha_{3}$ 和基 $\beta_{1}$ ， $\beta_{2}$ ， $\beta_{3}$ 下的坐标相同，所有非零向量为 $\xi = c \alpha_{1} - c \alpha_{3}$ ，其中 $c$ 为非零常数。

【解析】
(1) 由 $(\beta_1, \beta_2, \beta_3) = (\alpha_1, \alpha_2, \alpha_3) \begin{pmatrix} 2 & 0 & 1 \\ 0 & 2 & 0 \\ 2k & 0 & k+1 \end{pmatrix}$ ，计算矩阵行列式：

\left| \begin{pmatrix} 2 & 0 & 1 \\ 0 & 2 & 0 \\ 2k & 0 & k+1 \end{pmatrix} \right| = 2 \times 2 \times [(2)(k+1) - 1 \times 2k] = 4 \neq 0

故向量组 $\beta_1$ 、 $\beta_2$ 、 $\beta_3$ 线性无关，为向量空间 $\mathbb{R}^{3}$ 的一组基。

(2) 设非零向量 $\xi$ 在两组基下的坐标都是 $(x_1, x_2, x_3)$ ，则：

x_1 \alpha_1 + x_2 \alpha_2 + x_3 \alpha_3 = x_1 \beta_1 + x_2 \beta_2 + x_3 \beta_3

整理得：

x_1 (-\alpha_1 - 2k \alpha_3) + x_2 (-2 \alpha_2) + x_3 (-\alpha_1 - k \alpha_3) = 0

即：

(-\alpha_1 - 2k \alpha_3, -2 \alpha_2, -\alpha_1 - k \alpha_3) \begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix} = 0

该齐次线性方程组有非零解的充要条件是系数矩阵行列式为零：

\left| \begin{pmatrix} -1 & 0 & -1 \\ 0 & -2 & 0 \\ -2k & 0 & -k \end{pmatrix} \right| = (-1) \times (-2) \times [(-1)(-k) - (-1)(-2k)] = 2 \times (-k) = 0

解得 $k = 0$ 。此时方程组为：

(-\alpha_1, -2 \alpha_2, -\alpha_1) \begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix} = 0

即：

\begin{cases} -x_1 - x_3 = 0 \\ -2x_2 = 0 \end{cases}

通解为 $x_1 = c$ ， $x_2 = 0$ ， $x_3 = -c$ （ $c \neq 0$ ），故所有非零向量为 $\xi = c \alpha_1 - c \alpha_3$ （ $c$ 为非零常数）。

21

（本题满分 11 分）已知矩阵 $A = \begin{pmatrix} 0 & 2 & -3 \\ -1 & 3 & -3 \\ 1 & -2 & a \end{pmatrix}$ 与 $B = \begin{pmatrix} 1 & -2 & 0 \\ 0 & b & 0 \\ 0 & 3 & 1 \end{pmatrix}$ 相似。

(1) 求 $a$ ， $b$ 的值；

(2) 求可逆矩阵 $P$ ，使 $P^{-1}AP$ 为对角矩阵。

线性代数矩阵的相似与相似对角化

【答案】
(1) $a = 4$ ， $b = 5$
(2) $P = \begin{pmatrix} 2 & -3 & 1 \\ 1 & 0 & -2 \\ 0 & 1 & 1 \end{pmatrix}$

【解析】
(1) 因为矩阵 $A$ 与 $B$ 相似，所以迹相等且行列式相等，即

\begin{cases} 0 + 3 + a = 1 + b + 1 \\ |A| = |B| \end{cases}

计算行列式： $|A| = \begin{vmatrix} 0 & 2 & -3 \\ -1 & 3 & -3 \\ 1 & -2 & a \end{vmatrix} = 0 \cdot \begin{vmatrix} 3 & -3 \\ -2 & a \end{vmatrix} - 2 \cdot \begin{vmatrix} -1 & -3 \\ 1 & a \end{vmatrix} (-3) \cdot \begin{vmatrix} -1 & 3 \\ 1 & -2 \end{vmatrix} = -2(-a + 3) - 3(2 - 3) = 2a - 6 + 3 = 2a - 3$

|B| = \begin{vmatrix} 1 & -2 & 0 \\ 0 & b & 0 \\ 0 & 3 & 1 \end{vmatrix} = 1 \cdot b \cdot 1 = b

因此得到方程组：

\begin{cases} 3 + a = 2 + b \\ 2a - 3 = b \end{cases}

解得 $a = 4$ ， $b = 5$ 。

(2) 由 $B$ 的特征值为其对角元素 $1$ （二重）和 $5$ ，故 $A$ 的特征值也为 $1$ （二重）和 $5$ 。

对于特征值 $\lambda = 1$ ，解方程组 $(E - A)x = 0$ ：

E - A = \begin{pmatrix} 1 & -2 & 3 \\ 1 & -2 & 3 \\ -1 & 2 & -3 \end{pmatrix}

经初等行变换得：

\begin{pmatrix} 1 & -2 & 3 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{pmatrix}

基础解系为：

\xi_{1} = \begin{pmatrix} 2 \\ 1 \\ 0 \end{pmatrix}, \quad \xi_{2} = \begin{pmatrix} -3 \\ 0 \\ 1 \end{pmatrix}

对于特征值 $\lambda = 5$ ，解方程组 $(5E - A)x = 0$ ：

5E - A = \begin{pmatrix} 5 & -2 & 3 \\ 1 & 2 & 3 \\ -1 & 2 & 1 \end{pmatrix}

经初等行变换得：

\begin{pmatrix} 1 & 0 & -1 \\ 0 & 1 & 2 \\ 0 & 0 & 0 \end{pmatrix}

基础解系为：

\xi_{3} = \begin{pmatrix} 1 \\ -2 \\ 1 \end{pmatrix}

令 $P = (\xi_{1}, \xi_{2}, \xi_{3}) = \begin{pmatrix} 2 & -3 & 1 \\ 1 & 0 & -2 \\ 0 & 1 & 1 \end{pmatrix}$ ，则

P^{-1}AP = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 5 \end{pmatrix}

22

（本题满分 11 分）设 $f(x)= \begin{cases}2^{-x} \ln 2, & x>0 \\ 0, & x \leq 0\end{cases}$ ，对 $X$ 进行独立重复的观测，直到第 2 个大于 3 的观测值出现时停止，记 $Y$ 为观测次数。求：

(1) 求 $Y$ 的概率分布；

(2) 求数学期望 $E(Y)$ 。

概率论与数理统计随机变量及其分布

【答案】
(1) $P(Y=k) = \frac{1}{64}(k-1)\left(\frac{7}{8}\right)^{k-2}, \quad k=2,3,4,\ldots$
(2) $E(Y) = 16$

【解析】
(1) 对 $X$ 进行独立重复的观测，得到观测值大于 3 的概率为

P(X>3)=\int_{3}^{+\infty} 2^{-x} \ln 2 \, dx=\frac{1}{8}

显然 $Y$ 的可能取值为 $2,3,4,\ldots$

且

P(Y=k)=\frac{1}{8} \times C_{k-1}^{1} \frac{1}{8} \times\left(\frac{7}{8}\right)^{k-2}=\frac{1}{64}(k-1)\left(\frac{7}{8}\right)^{k-2}, \quad k=2,3,4,\ldots

(2) 设

\begin{align*} S(x) &= \sum_{n=2}^{\infty} n(n-1) x^{n-2} \\ &= \sum_{n=2}^{\infty} \left( x^{n} \right)'' \\ &= \left( \sum_{n=2}^{\infty} x^{n} \right)'' \\ &= \left( \frac{x^{2}}{1-x} \right)'' \\ &= \frac{2}{(1-x)^{3}}, \quad |x|<1 \end{align*}

E(Y)=\sum_{k=2}^{\infty} k P(Y=k)=\sum_{n=2}^{\infty} \frac{1}{64} k(k-1)\left(\frac{7}{8}\right)^{k-2}=\frac{1}{64} S\left(\frac{7}{8}\right)=16

23

（本题满分 11 分）设总体 $X$ 的概率密度为

f(x ; \theta) = \begin{cases} \dfrac{1}{1 - \theta}, & \theta \leq x \leq 1 \\ 0, & \text{其他} \end{cases}

其中 $\theta$ 为未知参数， $x_{1}, x_{2}, \cdots, x_{n}$ 是来自总体的简单样本。

(1) 求参数 $\theta$ 的矩估计量；

(2) 求参数 $\theta$ 的最大似然估计量。

概率论与数理统计参数估计与假设检验矩估计和最大似然估计

【答案】
(1) 矩估计量： $\hat{\theta} = 2\bar{x} - 1$
(2) 最大似然估计量： $\hat{\theta} = \min(x_{1}, x_{2}, \cdots, x_{n})$

【解析】
(1) 总体的数学期望为
$E(X) = \int_{\theta}^{1} x \cdot \frac{1}{1-\theta} \, dx = \frac{1}{2}(1+\theta)$ 。

令 $E(X) = \bar{X}$ ，解得参数 $\theta$ 的矩估计量为
$\hat{\theta} = 2\bar{x} - 1$ 。

(2) 似然函数为

L(x_{1}, x_{2}, \cdots, x_{n}; \theta) = \begin{cases} \frac{1}{(1-\theta)^{n}}, & \theta \leq x_{1}, x_{2}, \cdots, x_{n} \leq 1 \\ 0, & \text{} \end{cases}

显然 $L(\theta)$ 是关于 $\theta$ 的单调递增函数。为了使似然函数达到最大，只要使参数 $\theta$ 尽可能大即可，因此参数 $\theta$ 的最大似然估计量为
$\hat{\theta} = \min(x_{1}, x_{2}, \cdots, x_{n})$ 。