2008 年真题
选择题
1
设函数
f(x)=∫0x2ln(2+t)dt
,则
f′(x)
的零点个数为()。
正确答案:Bf′(x)=[ln(2+x2)]⋅2x
,
f′(0)=0
,即
x=0
是
f′(x)
的一个零点。
又
f′′(x)=2ln(2+x2)+2+x24x2>0
,从而
f′(x)
单调递增
(x∈(−∞,+∞))
。
所以
f′(x)
只有一个零点。
2
函数
f(x,y)=arctanyx
在点
(0,1)
处的梯度等于 ( )
正确答案:A因为
fx′=1+x2/y21/y
,
fy′=1+x2/y2−x/y2
,
所以
fx′(0,1)=1
,
fy′(0,1)=0
,
因此
gradf(0,1)=1⋅i+0⋅j=i
。
3
在下列微分方程中,以
y=C1ex+C2cos2x+C3sin2x
(
C1
、
C2
、
C3
为任意常数)为通解的是( )
正确答案:D由微分方程的通解中含有
ex
、
cos2x
、
sin2x
可知,齐次线性方程所对应的特征方程有根
r=1
,
r=±2i
。
因此,特征方程为:
(r−1)(r−2i)(r+2i)=0
展开得:
r3−r2+4r−4=0
故以已知函数为通解的微分方程为:
y′′′−y′′+4y′−4y=0
4
设函数
f(x)
在
(−∞,+∞)
内单调有界,
{xn}
为数列,下列命题正确的是( )
正确答案:B
因为
f(x)
在
(−∞,+∞)
内单调有界,且
{xn}
单调,所以
{f(xn)}
单调且有界,故
{f(xn)}
一定存在极限。
5
设
A
为
n
阶非零矩阵,
E
为
n
阶单位矩阵,若
A3=0
,则( )
正确答案:C
(E−A)(E+A+A2)=E−A3=E
,
(E+A)(E−A+A2)=E+A3=E
,
故
E−A
与
E+A
均可逆。
6
设二次型
f(x,y,z)=XTAX
(
X=(x,y,z)T
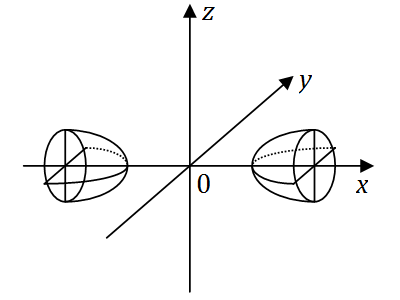
)的图形如图,则
A
的正特征值个数为( )
正确答案:B图示的二次曲面为双叶双曲面,其方程为
a2x′2−b2y′2−c2z′2=1,
即二次型的标准形为
f=a2x′2−b2y′2−c2z′2.
因此,正惯性指数为
1
,说明矩阵
A
的正特征值个数为
1
。
7
设随机变量
X
、
Y
独立同分布,且
X
的分布函数为
F(x)
,则
Z=max{X,Y}
的分布函数为( )
正确答案:A
FZ(x)=P(Z≤x)=P{max{X,Y}≤x}=P(X≤x)P(Y≤x)=F(x)F(x)=F2(x)
8
设随机变量
X∼N(0,1)
,
Y∼N(1,4)
且相关系数
ρXY=1
,则()
正确答案:D用排除法,设
Y=aX+b
。
由
ρXY=1
,可知
X
与
Y
正相关,得
a>0
,排除 (A) 和 (C)。
由
X∼N(0,1)
,
Y∼N(1,4)
,得
E(X)=0
,
E(Y)=1
。
于是
E(Y)=E(aX+b)=aE(X)+b=a×0+b=1,
所以
b=1
,排除 (B)。
故选择 (D)。
填空题
9
(填空题)微分方程
xy′+y=0
满足条件
y(1)=1
的解是
y=
【答案】
y=x1
【解析】 由
dxdy=x−y
分离变量积分得
−ln∣y∣=ln∣x∣+C1
,
所以
∣y∣1=∣x∣⋅C
。
又
y(1)=1
,
所以
y=x1
。
10
(填空题)曲线
sin(xy)+ln(y−x)=x
在点
(0,1)
处的切线方程为
【答案】
y=x+1
【解析】 设
F(x,y)=sin(xy)+ln(y−x)−x
,则
dxdy=−Fy′Fx′=−xcos(xy)+y−x1ycos(xy)−y−x1−1
将
y(0)=1
代入得
故切线方程为
y−1=x−0
即
y=x+1
11
(填空题)已知幂级数
∑n=0∞an(x+2)n
在
x=0
处收敛,在
x=−4
处发散,则幂级数
∑n=0∞an(x−3)n
的收敛域为()
【答案】
(1,5]
【解析】
幂级数
∑n=0∞an(x+2)n
的收敛区间以
x=−2
为中心。
由于该级数在
x=0
处收敛,在
x=−4
处发散,因此其收敛半径为
2
,收敛域为
(−4,0]
。
即当
−2<x+2≤2
时级数收敛,亦即
∑n=0∞antn
的收敛半径为
2
,收敛域为
(−2,2]
。
对于
∑n=0∞an(x−3)n
,其收敛半径仍为
2
。
由
−2<x−3≤2
可得
1<x≤5
,
因此幂级数
∑n=0∞an(x−3)n
的收敛域为
(1,5]
。
12
(填空题)设曲面
Σ
是
z=4−x2−y2
的上侧,则
∬Σxydydz+xdzdx+x2dxdy=
【答案】 4π
【解析】 给定曲面
∑1:z=0
(其中
x2+y2≤4
)的下侧,记
∑
与
∑1
所围成的空间区域为
Ω
。
则原式可表示为:
∬∑+∑1(xydydz+xdzdx+x2dxdy)−∬∑1(xydydz+xdzdx+x2dxdy)
利用高斯公式,第一项化为:
∭Ωydxdydz
第二项由于
∑1
取下侧,其法向量与
z
轴反向,故:
∬x2+y2≤4x2dxdy
因此原式等于:
∭Ωydxdydz−(−∬x2+y2≤4x2dxdy)
由于
Ω
关于
x
轴对称且被积函数
y
为奇函数,故:
∭Ωydxdydz=0
剩余部分为:
∬x2+y2≤4x2dxdy
利用对称性:
∬x2+y2≤4x2dxdy=21∬x2+y2≤4(x2+y2)dxdy
转换为极坐标:
21∫02πdθ∫02r3dr=21⋅2π⋅416=4π
最终结果为:
4π
13
(填空题)设
A
为
2
阶矩阵,
α1
,
α2
为线性无关的
2
维列向量,
Aα1=0
,
Aα2=2α1+α2
,则
A
的非零特征值为()
【答案】 1
【解析】 由
A(α1,α2)=(α1,α2)(0021)
,记
P=(α1,α2)
,
B=(0021)
,则
A
与
B
相似。
由
∣λE−B∣=λ(λ−1)=0
,得
B
的特征值为
0
和
1
,故
A
的非零特征值为
1
。
14
(填空题)设随机变量
X
服从参数为
1
的泊松分布,则
P{X=EX2}=
______
【答案】
2e1
【解析】 由
DX=EX2−(EX)2
,
X
服从参数为 1 的泊松分布,故
DX=EX=1
。
所以
EX2=1+1=2
,则
P{X=2}=2!12e−1=2e1
。
解答题
15
(本题满分 9 分)
求极限
x→0limx4[sinx−sin(sinx)]sinx
【答案】
61
【解析】 方法一:
x→0limx4[sinx−sin(sinx)]sinx=x→0limx3sinx−sin(sinx)=x→0lim3x2cosx−cos(sinx)cosx=x→0lim3x21−cos(sinx)=x→0lim3x221sin2x=61
方法二:
∵sinxsin(sinx)=x−61x3+o(x3),=sinx−61sin3x+o(sin3x)
∴x→0limx4[sinx−sin(sinx)]sinx=x→0lim[6x4sin4x+x4o(sin4x)]=61
16
(本题满分 9 分)
计算曲线积分
∫Lsin2xdx+2(x2−1)ydy
,其中
L
是曲线
y=sinx
上从点
(0,0)
到点
(π,0)
的一段。
【答案】
−2π2
【解析】 方法一:(直接取
x
为参数,将对坐标的曲线积分化成定积分计算)
∫Lsin2xdx+2(x2−1)ydy=∫0π[sin2x+2(x2−1)sinx⋅cosx]dx=∫0πx2sin2xdx=−2x2cos2x0π+∫0πxcos2xdx=−2π2+2xsin2x0π−21∫0πsin2xdx=−2π2 方法二:(添加
x
轴上的直线段,用格林公式化成二重积分计算)
取
L1
为
x
轴上从点
(π,0)
到点
(0,0)
的一段,
D
是由
L
与
L1
围成的区域。
∫Lsin2xdx+2(x2−1)ydy=∫L+L1sin2xdx+2(x2−1)ydy−∫L1sin2xdx+2(x2−1)ydy=−∬D4xydxdy−∫π0sin2xdx=−∫0πdx∫0sinx4xydy−21cos2x0π=−∫0π2xsin2xdx=−∫0πx(1−cos2x)dx=−2x20π+2xsin2x0π−21∫0πsin2xdx=−2π2 方法三:(将其拆成
∫Lsin2xdx−2ydy+∫L2x2ydy
,前者与路径无关,选择沿
x
轴上的直线段积分,后者化成定积分计算)
∫Lsin2xdx+2(x2−1)ydy=∫Lsin2xdx−2ydy+∫L2x2ydy=I1+I2
对于
I1
,因为
∂y∂P=∂x∂Q=0
,故曲线积分与路径无关,取
(0,0)
到
(π,0)
的直线段积分。
I1=∫0πsin2xdx=0
I2=∫L2x2ydy=∫0π2x2sinxcosxdx=∫0πx2sin2xdx=−21∫0πx2dcos2x=−21x2cos2x0π+21∫0π2xcos2xdx=−21π2+21∫0πxdsin2x=−21π2+21[xsin2x+21cos2x]0π=−21π2 所以,原式
=−21π2
。
17
(本题满分 11 分)
已知曲线
C:{x2+y2−2z2=0x+y+3z=5
,求曲线
C
距离
XOY
面最远的点和最近的点。
【答案】 最远点为
(−5,−5,5)
,最近点为
(1,1,1)
。
【解析】
点
(x,y,z)
到
xOy
面的距离为
∣z∣
,故求
C
上距离
xOy
面的最远点和最近点的坐标,等价于求函数
H=z2
在条件
x2+y2−2z2=0
与
x+y+3z=5
下的最大值点和最小值点。
令
L(x,y,z,λ,μ)=z2+λ(x2+y2−2z2)+μ(x+y+3z−5)
则有
⎩⎨⎧Lx′=2λx+μ=0Ly′=2λy+μ=0Lz′=2z−4λz+3μ=0x2+y2−2z2=0x+y+3z=5(1)(2)(3)(4)(5) 由 (1) 和 (2) 得
x=y
,代入 (4) 和 (5) 得
{x2−z2=02x+3z=5
解得
⎩⎨⎧x=−5y=−5z=5或⎩⎨⎧x=1y=1z=1 18
(本题满分 10 分)
设
f(x)
是连续函数,
(1) 利用定义证明函数
F(x)=∫0xf(t)dt
可导,且
F′(x)=f(x)
;
(2) 当
f(x)
是以
2
为周期的周期函数时,证明函数
G(x)=2∫0xf(t)dt−x∫02f(t)dt
也是以
2
为周期的周期函数。
【答案】 见解析
【解析】
(1) 对任意的
x
,由于
f
是连续函数,所以
Δx→0limΔxF(x+Δx)−F(x)=Δx→0limΔx∫0x+Δxf(t)dt−∫0xf(t)dt=Δx→0limΔx∫xx+Δxf(t)dt=Δx→0limΔxf(ξ)Δx=Δx→0limf(ξ), ξ x x+Δx
由于
limΔx→0f(ξ)=f(x)
,可知函数
F(x)
在
x
处可导,且
F′(x)=f(x)
。
(2) 方法一:要证明
G(x)
以
2
为周期,即要证明对任意的
x
,都有
G(x+2)=G(x)
。
令
H(x)=G(x+2)−G(x)
,则
H′(x)=(2∫0x+2f(t)dt−(x+2)∫02f(t)dt)′−(2∫0xf(t)dt−x∫02f(t)dt)′=2f(x+2)−∫02f(t)dt−2f(x)+∫02f(t)dt=0
又因为
H(0)=G(2)−G(0)=(2∫02f(t)dt−2∫02f(t)dt)−0=0
所以
H(x)=0
,即
G(x+2)=G(x)
。
方法二:由于
f
是以
2
为周期的连续函数,所以对任意的
x
,有
G(x+2)−G(x)=2∫0x+2f(t)dt−(x+2)∫02f(t)dt−2∫0xf(t)dt+x∫02f(t)dt=2[∫02f(t)dt+∫2x+2f(t)dt−∫0xf(t)dt]=2[−∫0xf(t)dt+∫0xf(u+2)du]=2∫0x[f(t+2)−f(t)]dt=0
即
G(x)
是以
2
为周期的周期函数。
19
(本题满分
11
分)
将
f(x)=1−x2 (0≤x≤π)
展开为余弦级数,并求级数
∑n=1∞n2(−1)n−1
的和。
【答案】
∑n=1∞n2(−1)n−1=12π2
【解析】
由于
a0=π2∫0π(1−x2)dx=2−32π2,
an=π2∫0π(1−x2)cosnxdx=(−1)n+1n24(n=1,2,…),
所以
f(x)=2a0+n=1∑∞ancosnx=1−3π2+4n=1∑∞n2(−1)n+1cosnx(0≤x≤π).
令
x=0
,有
f(0)=1−3π2+4n=1∑∞n2(−1)n+1.
又
f(0)=1
,所以
n=1∑∞n2(−1)n+1=12π2.
20
(本题满分 10 分)
设
α,β
为 3 维列向量,矩阵
A=ααT+ββT
,其中
αT,βT
分别是
α,β
的转置。证明:
(Ⅰ)
r(A)≤2
;
(Ⅱ)若
α,β
线性相关,则秩
r(A)<2
。
【答案】 见解析
【解析】
(I) 我们有
r(A)=r(ααT+ββT)≤r(ααT)+r(ββT)≤r(α)+r(β)≤2
。
(II) 由于
α
、
β
线性相关,不妨设
α=kβ
。于是
r(A)=r(ααT+ββT)=r((1+k2)ββT)≤r(β)≤1<2
。
21
(本题满分 12 分)
设
n
元线性方程组
Ax=b
,其中
A=2aa212aa212a⋱⋱⋱a212a,x=x1x2⋮xn,b=10⋮0. (Ⅰ) 证明行列式
∣A∣=(n+1)an
;
(Ⅱ) 当
a
为何值时,该方程组有唯一解,并求
x1
;
(Ⅲ) 当
a
为何值时,该方程组有无穷多解,并求通解。
【答案】
(Ⅰ)见解析
(Ⅱ)当
a=0
时,方程组有唯一解,且
x1=(n+1)an
(Ⅲ)当
a=0
时,方程组有无穷多解,且通解为
x=010⋮0+k100⋮0
,其中
k
为任意常数。
【解析】
(Ⅰ)证明
记
Dn=∣A∣=2aa212aa212a⋱⋱⋱a212an, 下面用数学归纳法证明
Dn=(n+1)an
。
当
n=1
时,
D1=2a
,结论成立。
当
n=2
时,
结论成立。
假设结论对小于
n
的情况成立,将
Dn
按第一行展开,得
Dn=2aDn−1−a2012aa212a⋱⋱⋱a212an−1. 第二个行列式等于
a2Dn−2,
因此
Dn=2aDn−1−a2Dn−2.
代入归纳假设
Dn−1=nan−1,Dn−2=(n−1)an−2,
得
Dn=2a⋅nan−1−a2⋅(n−1)an−2=(n+1)an.
故
∣A∣=(n+1)an.
(Ⅱ)解
当
a=0
时,方程组系数行列式
Dn=0
,故方程组有唯一解。
由 Cramer 法则,将
Dn
的第一列换成
b
,得行列式
Δ1=10a212a2a⋱11⋱a2⋱2aa212an. 按第一列展开,等于
2aa212aa212a⋱⋱⋱a212an−1=Dn−1. 已知
Dn−1=nan−1,
因此
x1=DnΔ1=(n+1)annan−1=(n+1)an.
(Ⅲ)解
当
a=0
时,方程组化为
0101⋱⋱010x1x2⋮xn−1xn=10⋮00. 系数矩阵的秩与增广矩阵的秩均为
n−1
,方程组有无穷多解,通解为
x=(0,1,0,…,0)T+k(1,0,0,…,0)T,
其中
k
为任意常数。
22
(本题满分 11 分)
设随机变量
X
与
Y
相互独立,
X
的概率分布为
P{X=i}=31 (i=−1,0,1)
,
Y
的概率密度为
fY(y)={1,0,0≤y<1其他
记
Z=X+Y
。
(Ⅰ) 求
P{Z≤21X=0}
;
(Ⅱ) 求
Z
的概率密度
fZ(z)
。
【答案】
(Ⅰ)
P{Z≤21X=0}=21
(Ⅱ)
fZ(z)={31,0,−1≤z<2其他
【解析】
(1)
P{Z≤21X=0}=P(X+Y≤21X=0)=P(X=0)P(X=0,Y≤21)=P(Y≤21)=∫0211dy=21. (2)
FZ(z)=P{Z≤z}=P{X+Y≤z}=31[P{Y≤z+1}+P{Y≤z}+P{Y≤z−1}]=31[FY(z+1)+FY(z)+FY(z−1)],
所以
fZ(z)=31[fY(z+1)+fY(z)+fY(z−1)]={31,0,−1≤z<2,otherwise.
23
(本题满分 11 分)
设
X1,X2,⋯,Xn
是总体
N(μ,σ2)
的简单随机样本,记
Xˉ=n1∑i=1nXi
,
S2=n−11∑i=1n(Xi−Xˉ)2
,
T=Xˉ2−n1S2
。
(Ⅰ)证明
T
是
μ2
的无偏估计量;
(Ⅱ)当
μ=0
,
σ=1
时,求
D(T)
。
【答案】
(Ⅰ)见解析
(Ⅱ)
D(T)=n(n−1)2
【解析】
(1) 因为
X∼N(μ,σ2)
,所以
Xˉ∼N(μ,nσ2)
,从而
EXˉ=μ
,
DXˉ=nσ2
。
于是有:
E(T)=E(Xˉ2−n1S2)=EXˉ2−n1E(S2)=DXˉ+(EXˉ)2−n1E(S2)=n1σ2+μ2−n1σ2=μ2,
因此
T
是
μ2
的无偏估计量。
(2) 方法一:由
D(T)=ET2−(ET)2
,当
μ=0
,
σ=1
时,
E(T)=0
,
E(S2)=σ2=1
。
计算可得:
E(Xˉ4)=n23,ES4=n−1n+1,
于是:
ET2=n23−n2⋅n1⋅1+n21⋅n−1n+1=n(n−1)2,
即
D(T)=n(n−1)2
。
方法二:当
μ=0
,
σ=1
时,有:
D(T)=D(Xˉ2−n1S2)=DXˉ2+n21DS2.
进一步计算:
DXˉ2=n21D(nXˉ)2=n21⋅2, DS2=(n−1)21D[(n−1)S2]=(n−1)21⋅2(n−1)=n−12,
所以:
D(T)=n22+n21⋅n−12=n(n−1)2.