这是本节的多页打印视图。 点击此处打印.

返回本页常规视图.

字符串

本章可能在选择题中出现，掌握 KMP 算法的思想，能够手工模拟 KMP 过程即可。

1 - 定义和实现

了解字符串的不同存储结构和基本操作即可，一般不会直接考察。

串的定义

字符串是计算机科学中的一个基本概念，通常被定义为 有限序列 中 字符 的有序集合。

形式定义：

字符串 $S$ 时 字符集 $\Sigma$ 上的一个 有限序列：$S = a_1 a_2 \cdots a_n$，其中 $a_i \in \Sigma$，且 长度 $n$ 为字符串的长度，
当 $n = 0$ 时，称为 空字符串。

串的存储结构

定长顺序存储表示

在 定长顺序存储表示 中，每个字符串都有固定的长度，通常用一个预定义的最大大小来表示。这种表示方法使用一个一维数组，数组的大小等于预定的最大长度。

在某些语境中（例如 C 语言），使用特殊字符（如 '\0'）来标识字符串结束。

#define MAX_SIZE 100 // 预定义的最大大小

typedef struct {
    char data[MAX_SIZE];  // 字符数组
    int length;           // 当前字符串的长度
} FixedString;

堆分配存储表示

在 堆分配存储表示 中，每个字符串具有其自己的 长度，因此可以动态地分配存储空间。字符串在堆中分配空间，只需要那么多的空间来存储实际的字符以及结束字符或 长度 信息。

typedef struct {
    char *data;           // 指向动态分配空间的指针
    int length;           // 字符串的长度
} HeapString;

// 创建一个新的字符串
void initHeapString(HeapString *s, const char *str) {
    s->length = strlen(str);
    s->data = (char *)malloc((s->length + 1) * sizeof(char));
    if (s->data == NULL) {
        exit(1);  // 分配失败
    }
    strcpy(s->data, str);
}

// 释放字符串
void freeHeapString(HeapString *s) {
    free(s->data);
    s->length = 0;
}

块链存储表示

块链存储表示 是结合了 链表 与 块 存储的思想。串分为较小的 块，每个块存储一部分 字符。块之间使用 指针 链接。这样，整个字符串就变成了一个字符块的链表。

#define BLOCK_SIZE 4 // 为了简单起见，设块大小为 4

typedef struct StringBlock {
    char data[BLOCK_SIZE];   // 块中的字符数据
    struct StringBlock *next;  // 指向下一个块的指针
} StringBlock;

typedef struct {
    StringBlock *head;      // 指向第一个块的指针
    int length;             // 字符串的总长度
} BlockString;

// 初始化块链字符串
void initBlockString(BlockString *s) {
    s->head = NULL;
    s->length = 0;
}

// 为了简化，这里只展示了数据结构定义和初始化函数。实际应用中还需要考虑其他函数，如插入、删除、销毁等。

串的基本操作

  • 赋值（Assign）：
    • 将一个串的内容复制到另一个串。
  • 比较（Compare）：
    • 根据字符的字典顺序比较两个串。可以判断两个串是否相等，或者一个串是否小于或大于另一个串。
  • 长度（Length）：
    • 返回串的 长度，即串中字符的数目。
  • 连接（Concat）：
    • 将两个串连接成一个新的串。例如，将串"Hello"和串"World"连接为"HelloWorld"。
  • 子串提取（Substr）：
    • 从串中提取某个指定位置开始的指定 长度 的字符序列作为一个新的串。例如，从串"HelloWorld"中提取从位置 1 开始的 5 个字符，得到"Hello"。
  • 插入（Insert）：
    • 在串的指定位置插入另一个串。例如，在串"HelloWorld"的第 6 个位置插入串"Beautiful", 得到"HelloBeautifulWorld"。
  • 删除（Delete）：
    • 从串中删除从指定位置开始的指定 长度 的字符。
  • 替换（Subsititude）：
    • 将串中某个子串的所有出现替换为另一个子串。例如，将串"apple, banana, apple"中的"apple"替换为"orange"，得到"orange, banana, orange"。
  • 模式匹配（Index）：
    • 在串中查找另一个子串的位置。这通常使用算法如 KMP、BM 或 Sunday 来加速查找。
  • 清空（Clear）：
    • 释放串的存储空间并将其设置为 空字符串。

2 - 模式匹配

需熟练掌握 KMP 算法，包含 next 数组的计算，以及手工模拟主串和模式串的移动过程，可能在选择题中考察。

字符串模式匹配 是计算机科学中的基础问题，主要是在一个 主字符串 中查找一个 子字符串 模式。

串概念

在介绍模式匹配算法之前，需要能够区分关于串的几个概念：

  • 主串（Str / 主字符串）：待搜索的那一整段字符串。
  • 子串（Substr / 子字符串）：主串中的某一段字符串
  • 模式串（Pattern / 模式字符串）：要在主串中查找的目标。

简单模式匹配算法

简单模式匹配算法（即暴力匹配 / 朴素匹配）的 基本思想 是：逐个检查 主串 的每一个位置，判断 从该位置开始的子串 是否与 模式串 完全相同。

算法描述：

  1. 从 主串 的第一个字符开始，尝试与 模式串 匹配。
  2. 如果当前字符匹配，则继续比较下一个字符，依此类推。
  3. 如果在某一位置发生不匹配，则将 模式串 移动到 主串 的下一个起始位置，重新匹配。
  4. 如果某一段 子串 与 模式串 完全相同，则返回该 子串在主串中的起始位置。
  5. 如果扫描完整个 主串 都没有找到匹配的 子串，则返回 -1。
int simplePatternMatching(const char* mainStr, const char* pattern) {
    int m = strlen(mainStr);
    int n = strlen(pattern);

    // 如果主字符串的长度小于模式字符串的长度，直接返回 -1
    if (m < n) return -1;

    for (int i = 0; i <= m - n; i++) {
        int j;
        for (j = 0; j < n; j++) {
            if (mainStr[i + j] != pattern[j]) {
                break;
            }
        }
        // 如果 j 等于模式串的长度，说明已经找到匹配
        if (j == n) return i;
    }
    return -1;  // 没有找到匹配
}

简单模式匹配算法的 核心思路 其实就是将主串中的每个字串和模式串进行对比。举个例子，主串 abaaabc 和模式串 abc 进行简单模式匹配的过程如下：

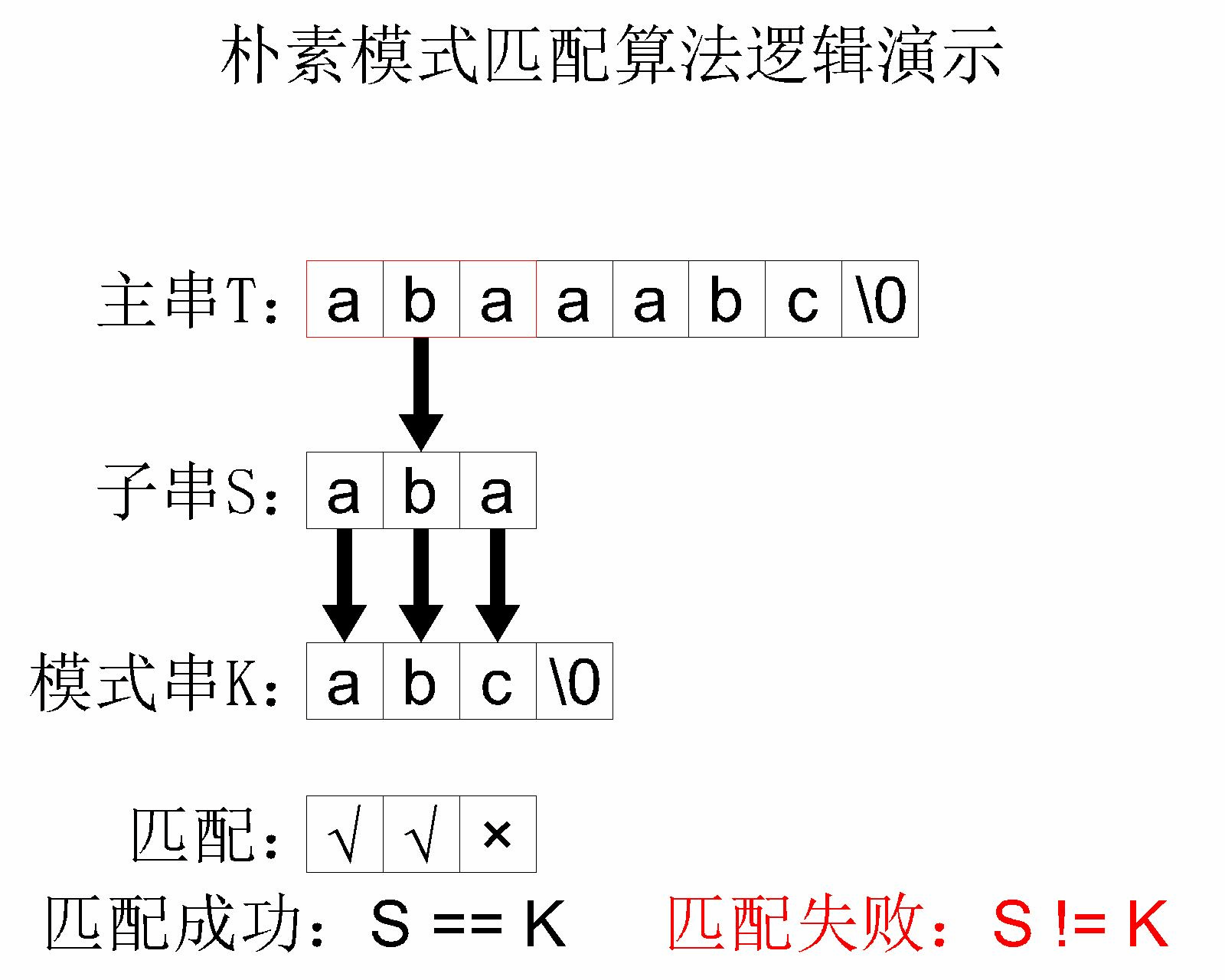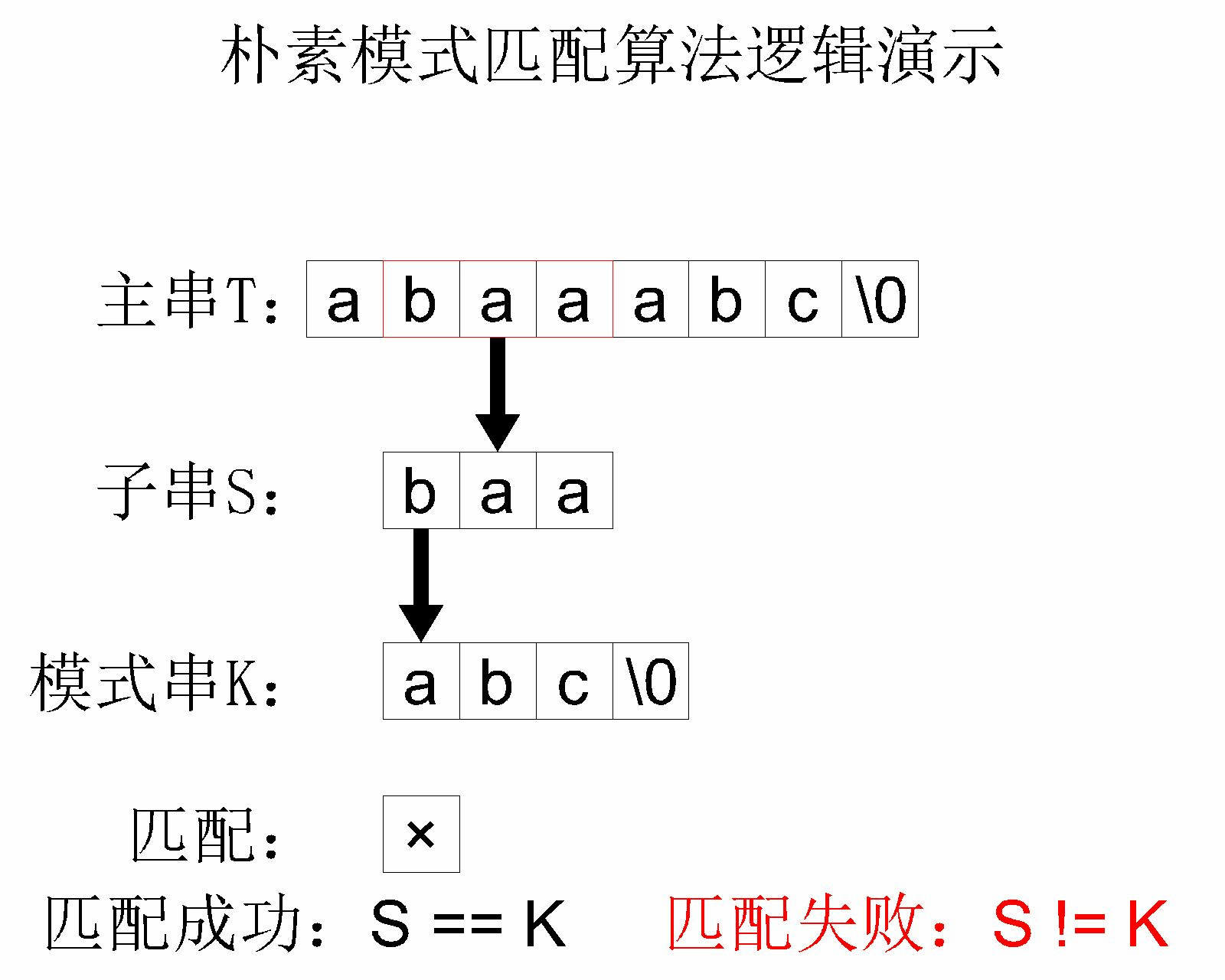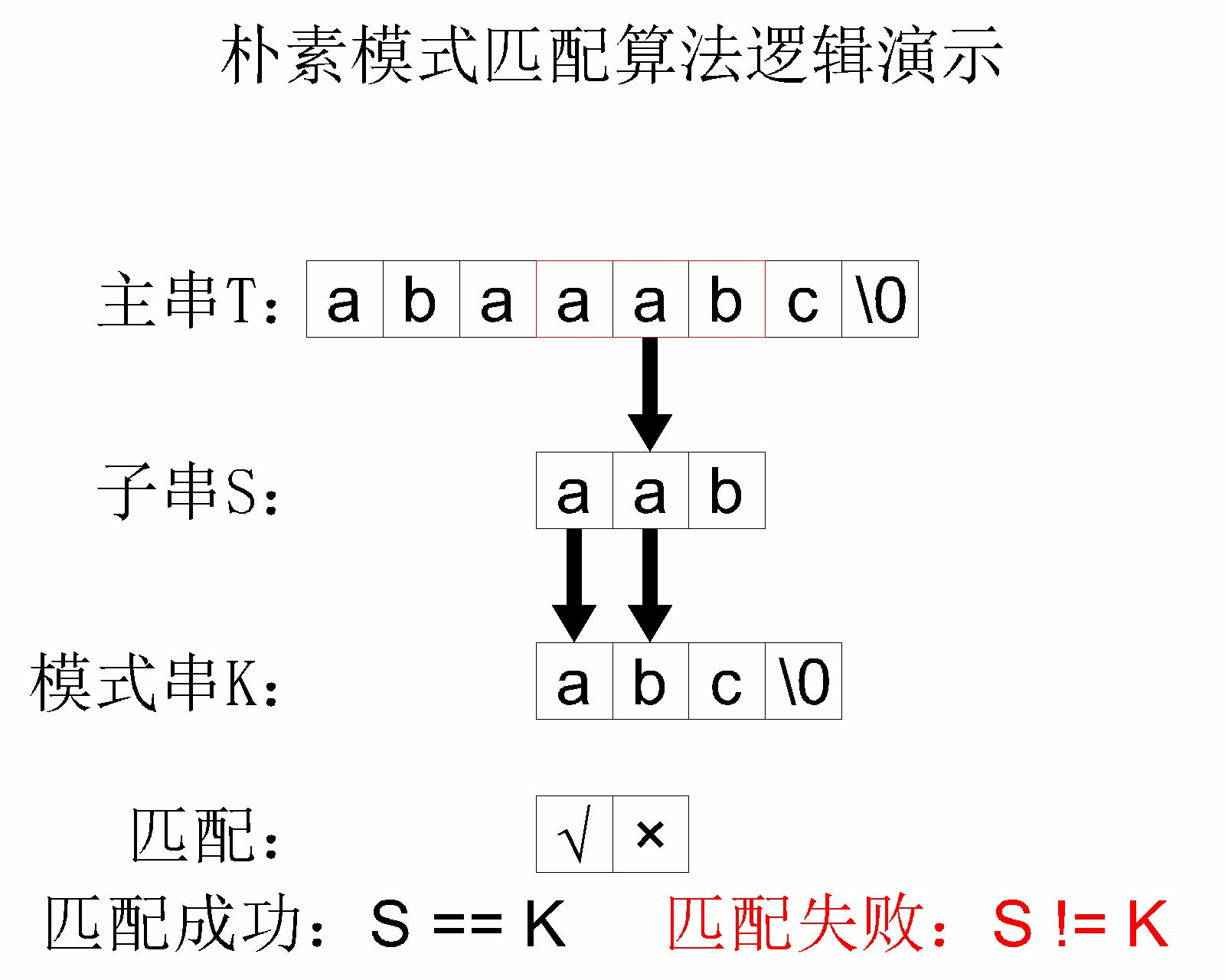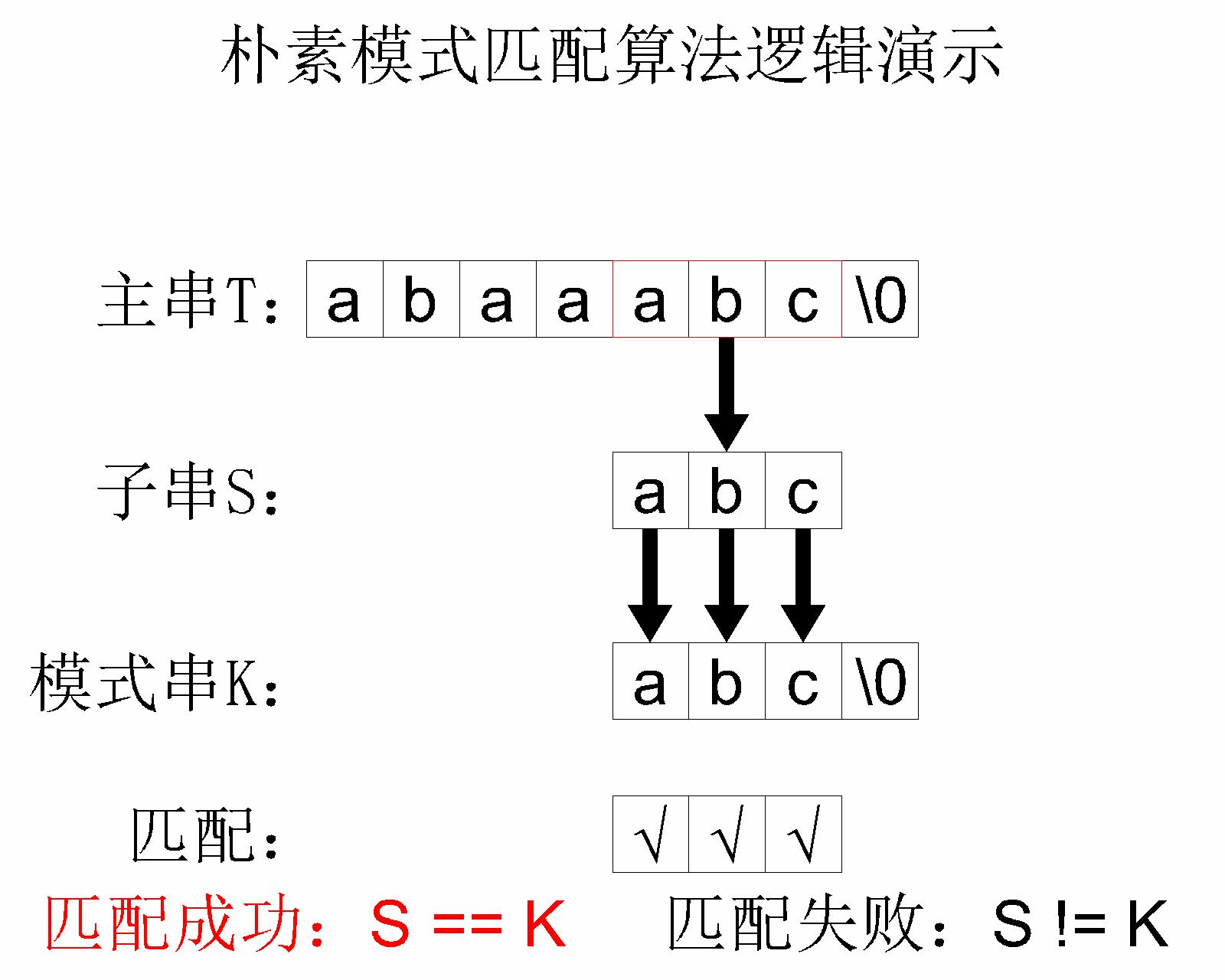
这个简单模式匹配算法的 时间复杂度 是 $O(mn)$，其中 $m$ 是 主字符串 的长度， $n$ 是 模式字符串 的长度。

KMP 算法

与 简单模式匹配算法 不同， KMP 算法 在发现不匹配的字符时能够避免不必要的比较，从而提高效率。

前后缀

简单模式匹配 时间复杂度过高，因为每一次匹配失败都得从下一个位置重新开始。这就没有充分应用 模式串 的特性，比如对于字符串 abcdabc，我们可以发现：

  • 其 前缀 包含a, ab, abc, abcd 等
  • 起 后缀 包含c, bc, abc, dabc 等

abc 是在其 前缀 和 后缀 中都包含的部分，在字符串匹配时，我们可以充分利用该信息，匹配失败时，我们可以不用从下一个位置开始，而是从 模式串内部的某个位置 开始。

KMP 算法 就是基于这个思想，其核心是一个称为 “部分匹配表” 或 “前缀函数” 的辅助数组（通常称为 next 数组），该数组用于确定当 模式串 在 主串 不匹配时应该如何有效地移动 模式串。

算法描述

  1. 构建 部分匹配表（next 数组）：next[i] 表示：当 模式串 在第 i 位 匹配失败 时，下一次 应该跳到的模式串位置。
  2. 不断进行 模式匹配，直到匹配成功或 主串 结束。

next 数组计算

如果 模式串 为 pattern，用通俗的话来说，next[k] 就是第 k 个字符的 前缀字符串 pattern[0:k-1]（pattern 的前 k 个字符构成的子串，不包含当前字符）的最长相同 前缀 和 后缀 的长度。

以 ababac 字符串为例，可以得到以下的 next 数组：

模式串（pattern）ababac
下标（index）012345
pattern[0:index] 的相同前后缀长度001230
next-100123

一般而言，next 数组 中的第一个元素被设置为 -1（因为第一个字符不存在 前缀子串）。

以 c 字符为例，我们需要计算 next[5]，所以需要统计 c 的 前缀字符串 ababa 的最长相同 前缀 和 后缀 的长度，可以观察到，最长的相同 前缀 和 后缀 为 aba，长度为 3，所以 next[5] = 3。

使用 next 调整位置

用 i 表示 主串 当前下标，用 j 表示 模式串 当前下标：

  • 如果 main[i] == pattern[j]，将 i 和 j 向后向后移动一位。
  • 如果 main[i] != pattern[j]：
    • 如果 j == 0，将 i 向后移动一位。
    • 如果 j != 0，将 j 移动到 next[j]。

以下图为例，说明 主串 “ababcabcabababd” 和 模式串 “ababd” 的匹配过程。

index
0
1
2
3
4
char
a
b
a
b
d
next
-1
0
0
1
2
a
b
a
b
c
a
b
c
a
b
a
b
a
b
d
string
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
a
b
a
b
d
i
j
a
b
a
b
d
j
a
b
a
b
d
j
a
b
a
b
c
a
b
c
a
b
a
b
a
b
d
string
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
i
a
b
a
b
d
j
pattern
pattern
字符串 "ababd" 对应的next数组
在 i = 4, j = 4 时匹配失败，
next[j] = next[4] = 2，
移动 j = 2
在 i = 4, j = 2 时匹配失败，
next[j] = next[2] = 0，
移动 j = 0
在 i = 4, j = 0 时匹配失败，
移动 i++, i = 5, j = 0
在 i = 5，j = 0 时匹配失败，
移动 i++
i = 6, j = 0

算法实现

算法实现了解即可，考试基本不会考察 kmp 算法 实现，只要能够熟练地在纸上模拟 kmp 算法 流程即可。

void computeNextArray(const char* pattern, int m, int* next) {
    int len = 0;
    next[0] = 0;
    int i = 1;

    while (i < m) {
        if (pattern[i] == pattern[len]) {
            len++;
            next[i] = len;
            i++;
        } else {
            if (len != 0) {
                len = next[len - 1];
            } else {
                next[i] = 0;
                i++;
            }
        }
    }
}

int KMP(const char* mainStr, const char* pattern) {
    int m = strlen(mainStr);
    int n = strlen(pattern);

    int next[n];
    computeNextArray(pattern, n, next);

    int i = 0, j = 0;
    while (i < m) {
        if (pattern[j] == mainStr[i]) {
            i++;
            j++;
        }

        if (j == n) {
            return i - j;
        } else if (i < m && pattern[j] != mainStr[i]) {
            if (j != 0)
                j = next[j - 1];
            else
                i++;
        }
    }

    return -1; // 没有找到匹配
}

修正后的 next 数组

其实上述内容就是 kmp 算法 的核心了，当然有时候也会涉及到这样一个概念： 修正后的 next 数组。

这个概念其实来源于早期教材（特别是严蔚敏的《数据结构》）， 修正后的 next 数组 常称作 nextval 数组，其目的是避免某些情况下的冗余匹配。

nextval 数组是为了修正 next 数组存在的以下问题：当 pattern[i] == pattern[next[i]] 时，如果直接使用 next[i]，会导致重复比较已经失败过的字符。

为了解决这个问题，定义了 nextval：其核心思想是：避免跳转到与当前位置字符相同的地方，减少无意义的重复比较。

  • 如果 pattern[i] == pattern[next[i]] → 则 nextval[i] = nextval[next[i]]
  • 否则 → nextval[i] = next[i]

nextval 的构建规则如下：

if (next[i] == -1) {
    nextval[i] = -1;
} else {
    int k = next[i];
    while (k != -1 && pattern[i] == pattern[k]) {
        k = nextval[k]; // 向前继续跳
    }
    nextval[i] = k;
}

需要注意的，nextval 的计算过程是迭代向前的，因为我们希望减少无意义的比较，所以要争取找到一个不同的字符。

以字符串 ababaa 为例，我们首先可以计算出其 next 数组：

patternababaa
index012345
next-100123

然后计算出 nextval 数组：

patternababaa
index012345
next-100003
  • nextval[0] = -1
  • nextval[1] = 0
  • nextval[2] = 0
  • pattern[3] = b, pattern[next[3]] = pattern[1] = b, 相等，优化：nextval[3] = nextval[1] = 0
  • pattern[4] = a, pattern[2] = a, 相等，优化：nextval[4] = nextval[2] = 0
  • nextval[5] = 3（pattern[5] = a, pattern[3] = b，不相等，保留原值）

其实 kmp 的现代实现中一般使用 next 数组 就足够了，nextval 主要是优化了极少数情况下的性能，特别是在大量重复字符的 模式串 里效果明显。