算法和应用

DFS

深度优先搜索（Depth-First Search，简称 DFS）是一种用于图的遍历和搜索的算法，它从图中的一个起始顶点开始，尽可能深地访问顶点，直到无法继续前进，然后回溯到之前的顶点，继续深入其他分支。DFS 通常用递归或栈来实现，确保在深度方向上优先遍历。

以下是 DFS 算法的一般步骤：

1. 从起始顶点开始，将其标记为已访问。
2. 遍历与当前顶点相邻的未访问顶点，选择其中一个未访问顶点作为下一个深度遍历的目标，然后递归地进行 DFS。
3. 如果无法继续深度遍历（即当前顶点没有未访问的邻居），则回溯到上一个顶点，继续遍历其他未访问的邻居。
4. 重复步骤 2 和步骤 3，直到所有顶点都被访问。

图中 DFS 实现的框架与 树的遍历 类似，不同点在于需要使用 visit 数组记录已经访问过的节点，避免重复遍历：

function DFS(G, v, visited):
    visited[v] ← true
    for each neighbor u of v in G.adjacent[v]:
        if not visited[u]:
            DFS(G, u, visited)

图在邻接矩阵和邻接表中的 DFS 都遵循这个框架，两者的不同点在于获取 v 的邻居 u 的方式不同。

邻接矩阵

在邻接矩阵中，我们定义一个递归函数 dfs，函数从 start 顶点出发，输出当前结点，然后递归地去访问所有与其相邻的顶点。

注意递归前需要保证下一个顶点未被访问过，这样可以避免重复访问结点以及死循环。

// 全局变量，标记顶点是否被访问过
int visited[MAX_VERTICES];

// 递归函数，从 start 顶点出发
void dfs(int start) {
    visited[start] = 1;
    printf("%d ", start);

    // 依次访问 start 的邻接顶点
    for (int i = 0; i < MAX_VERTICES; i++) {
        // 递归的两个条件：
        // 1. 顶点 (start, i) 之间存在边
        // 2. 顶点 i 未被访问过
        if (adjMatrix[start][i] == 1 && !visited[i]) {
            // 递归调用
            dfs(i);
        }
    }
}

邻接表

邻接表的递归思路与邻接矩阵一致，唯一的区别就是访问邻接顶点方式的不同。

在邻接矩阵中，通过遍历矩阵中的一行来访问相邻顶点。在邻接表中，通过遍历链表来访问相邻顶点。

// 全局变量，标记顶点是否被访问过
int visited[MAX_VERTICES];

// 递归函数，从 start 顶点出发
void dfs(struct Graph* graph, int start) {
    visited[start] = 1;
    printf("%d ", start);

    // 依次访问 start 的邻接顶点
    struct Node* temp = graph->adjacencyList[start];
    while (temp) {
        int adjVertex = temp->data;
        // 递归条件：顶点 i 未被访问过
        if (!visited[adjVertex]) {
            dfs(graph, adjVertex);
        }
        temp = temp->next;
    }
}

BFS

广度优先搜索（Breadth-First Search，简称 BFS）是一种用于图的遍历和搜索的算法，它从图中的一个起始顶点开始，逐层地访问与该顶点相邻的顶点，然后再访问这些相邻顶点的邻居，以此类推。BFS 通常用队列来实现，确保按照广度优先的顺序访问顶点。

以下是 BFS 算法的一般步骤：

1. 将起始顶点放入队列中，标记为已访问。
2. 从队列中弹出一个顶点并访问它。
3. 遍历该顶点的所有未被访问的邻居，将它们放入队列中，并标记为已访问。
4. 重复步骤 2 和步骤 3，直到队列为空。

BFS 的伪代码实现如下所示，基于邻接矩阵或邻接表的 BFS 都遵循这个框架：

function BFS(G, start):
    visited[start] ← true
    enqueue(Q, start)

    while Q is not empty:
        v ← dequeue(Q)
        process(v)
        for each neighbor u of v in G.adjacent[v]:
            if not visited[u]:
                visited[u] ← true
                enqueue(Q, u)

邻接矩阵

实现 bfs 时，首先添加起始顶点进入队列中，然后不断从队列中取出顶点，并添加该顶点的未访问相邻顶点进入队列。 重复直到队列为空。

在 dfs 中，visited 数组是各个递归函数都需要访问的数据结构，为了方便起见，可以定义为全局变量。 在 bfs 中，由于算法实现是基于迭代而非递归，所以 visited 和 队列 可以定义为局部变量。

// 从 start 开始遍历图
void bfs(int start, int vertices) {
    // 队列 q
    queue q;
    // 标记顶点是否被访问过
    int visited[MAX_VERTICES];
    // 添加初始顶点
    q.enqueue(start);
    visited[start] = 1;

    // 一直遍历到队列为空
    while (q.size() > 0) {
        // 从队列头部取出结点作为当前结点
        int currentVertex = q.dequeue();
        // 输出当前结点
        printf("%d ", currentVertex);
        // 将当前结点的所有 相邻的未访问顶点 添加到队列中
        for (int i = 0; i < vertices; i++) {
            if (adjMatrix[currentVertex][i] == 1 && !visited[i]) {
                q.enqueue(i);
                visited[i] = 1;
            }
        }
    }
}

邻接表

实现思路与邻接矩阵方式一致，不同点在与访问相邻顶点的方式不同。

void bfs(struct Graph* graph, int start) {
    // 队列 q
    queue q;
    // 标记顶点是否被访问过
    int visited[MAX_VERTICES];
    // 添加初始顶点
    q.enqueue(start);
    visited[start] = 1;

    // 一直遍历到队列为空
    while (front != rear) {
        // 从队列头部取出结点作为当前结点
        int currentVertex = q.dequeue();
        // 输出当前结点
        printf("%d ", currentVertex);
        // 将当前结点的所有 相邻的未访问顶点 添加到队列中
        struct Node* temp = graph->adjacencyList[currentVertex];
        while (temp) {
            int adjVertex = temp->data;
            if (!visited[adjVertex]) {
                q.enqueue(adjVertex);
                visited[adjVertex] = 1;
            }
            temp = temp->next;
        }
    }
}

最小生成树

最小生成树（Minimum Spanning Tree，MST）是在一个连接所有顶点的无向图中，通过选择一部分边而形成的树，使得树的总权重（或成本）最小。

准确的最小生成树定义如下：在无向图 $G = (V, E)$ 中，$(u, v)$ 代表连接顶点 $u$ 和顶点 $v$ 的边，而 $w(u, v)$ 代表此边的权重，若存在 $T$ 为 $E$ 的子集且 $(V, E)$ 为树，使得 $w(T) = \sum_{(u, v) \in T} w(u, v)$ 最小，则此 $T$ 为 $G$ 的最小生成树。

最小生成树满足以下特点：

• 包含图中的所有顶点。
• 通过选择一些边而形成一个树结构，没有环路。
• 边的总权重最小。

prim 算法

Prim 算法的主要思想是从一个初始顶点开始，逐步扩展生成树，每次选择与当前生成树相邻且权重最小的边所连接的顶点，并将该顶点加入生成树。算法的运行过程可以概括为以下步骤：

1. 选择一个起始顶点作为生成树的根节点。
2. 初始化一个空的生成树，包含初始顶点。
3. 将与生成树中的顶点相邻且权重最小的边的另一端顶点加入生成树，即选择一条最小权重边。
4. 重复步骤 3，直到生成树包含了所有的顶点。
5. 最终生成树即为原图的最小生成树。

kruskal 算法

Kruskal 算法是一种用于求解最小生成树（Minimum Spanning Tree，MST）的贪心算法。Kruskal 算法的基本思想是从边的权重最小的边开始，逐步构建生成树，确保不会形成环路。

以下是 Kruskal 算法的一般流程：

1. 初始化一个空的生成树，开始时生成树中没有边。
2. 将图中的所有边按照权重从小到大进行排序。
3. 依次从排序后的边列表中选取边，加入生成树，但要确保添加该边不会形成环路。可以使用并查集来检查是否形成环路。
4. 重复步骤 3，直到生成树包含了所有的顶点，即生成树中的边数等于顶点数减 1。
5. 返回生成树作为最小生成树。

最短路径

dijkstra 算法

Dijkstra 算法是一种用于计算 单源最短路径 的经典算法，适用于 带非负权重的有向或无向图。

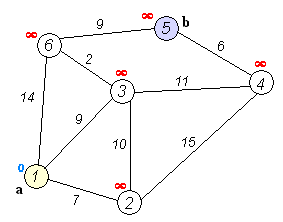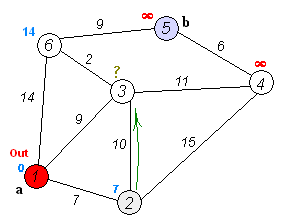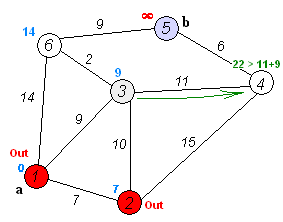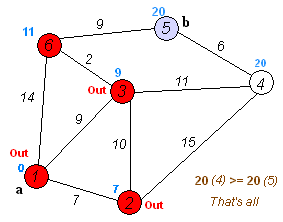
Dijkstra 算法是一种贪心算法。它从起点开始，维护一组已知的最短路径，每次从所有未处理的顶点中选择一个当前距离起点最短的顶点，将其加入“最短路径已确定”的集合，并通过它尝试更新其邻居的最短路径。该过程重复，直到所有顶点的最短路径都被确定。

🛠️ 算法需要定义以下数据结构：

• dist[]: 一个数组，dist[v] 表示起点到节点 v 的当前最短路径长度，初始化为 ∞，起点为 0。
• visited[]: 一个布尔数组，记录哪些节点的最短路径已被确定。

✨ 算法具体流程如下：

1. 初始化
   • dist[source] ← 0
   • 其他 dist[v] ← ∞
   • 所有 visited[v] ← false
2. 主循环（直到所有顶点都被访问）
   • 找出未访问的、dist[] 值最小的节点 u
   • 标记 visited[u] ← true
   • 对于 u 的每个邻居 v：
     • 如果 v 未访问，且 dist[u] + w(u,v) < dist[v]，则更新 dist[v] ← dist[u] + w(u,v)
3. 结束
   • 所有最短路径保存在 dist[] 中

Dijkstra 的考察侧重于手工模拟其过程，代码实现一般不会考察，这里给出算法的简单伪代码实现，帮助各位理清其中的处理细节。

function Dijkstra_Simple(Graph, source):
    对于图中每个顶点 v:
        dist[v] ← ∞          // 起点到 v 的距离初始化为无穷大
        visited[v] ← false   // 所有顶点初始都未被访问
    dist[source] ← 0         // 起点到自身距离为 0

    重复 |图中顶点数| 次:
        u ← 所有未访问的顶点中 dist[u] 最小的顶点
        visited[u] ← true    // 标记 u 已被访问

        对于 u 的每个相邻顶点 v:
            边权重 weight ← 图中边(u, v) 的权重
            如果 v 未访问 且 dist[v] > dist[u] + weight:
                dist[v] ← dist[u] + weight  // 通过 u 到 v 更短，更新最短路径

    return dist[] // 表示起点到所有顶点的最短路径

假设顶点的个数为 $V$，边的个数为 $E$，那么最佳实现（使用了优先队列）的 dijkstra 算法时间复杂度为 $O(V+E)$。

floyd 算法

Floyd Warshall 是一种基于动态规划的方法，用于求解任意两个顶点之间的最短路径，它适用于带权有向图。

该算法的核心思想是尝试使用每一个顶点作为中转点，逐步更新所有顶点对之间的最短路径。对任意两点 $i → j$，判断是否可以通过一个中间点 $k$ 得到更短路径：

$$dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j])$$

这个过程会遍历所有可能的中转点 $k$，不断优化路径。

✨ 算法具体流程如下：

1. 初始化距离矩阵 dist：
   • dist[i][j] = 0（若 i=j）
   • dist[i][j] = 边权（若 i→j 有边）
   • dist[i][j] = ∞（其余情况）
2. 三重循环更新最短路径

   for k in 所有顶点:
       for i in 所有顶点:
           for j in 所有顶点:
               if dist[i][k] + dist[k][j] < dist[i][j]:
                   dist[i][j] ← dist[i][k] + dist[k][j]
   

3. 输出 dist 矩阵 ：表示所有顶点对之间的最短路径长度。

若顶点数为 $n$，则 Floyd Warshall 算法的时间复杂度为 $O(n^3)$，该算法适合在算法题中兜底使用，因为实现比较简单，建议大家熟练掌握代码实现。

拓扑排序

拓扑排序这样一种对图中顶点的排序方式：

将图中的所有顶点排序，使得对于每一条有向边 u → v，顶点 u 都排在 v 之前。

拓扑排序主要应用于 DAG（有向无环图）或 AOV 网，这种图没有环路，因此可以对其进行拓扑排序。

首先需要区分 AOV 和 AOE 这两个概念，注意拓扑排序适用于 AOV，关键路径适用于 AOE。

AOV 网

AOV（Activity on Vertex Network）网是一种以顶点表示活动或任务的网络模型。每个顶点代表一个任务或活动，而边表示任务之间的依赖关系。在 AOV 网中，任务或活动通常表示为顶点，而依赖关系（任务的先后顺序）表示为有向边。

算法步骤

计算拓扑排序的算法有两种，一种是 Kahn 算法（基于入度），另一种是 DFS+栈 的实现。

Kahn 算法的核心思想是 依次选取入度为 0 的顶点进行输出，其具体步骤如下：

1. 选择一个没有前驱顶点（入度为 0）的顶点作为起始顶点，将其加入拓扑排序的结果序列中。
2. 从图中移除该顶点以及与之相关的边（即将与之相邻的顶点的入度减 1）。
3. 重复步骤 1 和步骤 2，直到所有的顶点都被加入到拓扑排序的结果序列中，或者发现图中存在环路。
4. 如果所有的顶点都被成功加入结果序列，那么这个序列就是拓扑排序的结果。

下图展示了一个采用 Kahn 算法输出 AOE 网中的拓扑序列的实例：

此外，可以通过 DFS+栈 得到拓扑序列，其步骤如下：

1. 对图进行深度优先遍历。
2. 每个节点 DFS 结束后将其压入栈中。
3. 最后将栈中元素逆序输出，就是拓扑排序结果。

DFS 过程中，每个节点在其所有后继节点访问完成后才被加入栈中，因此栈中元素的逆序正好满足拓扑排序所需的“前驱先于后继”的约束。

拓扑排序的时间复杂度通常为 $O(V + E)$ ，其中 $V$ 是顶点的数量， $E$ 是边的数量。这个算法非常适合于解决任务调度和依赖关系问题，因为它可以确定任务的执行顺序或依赖关系的合理性。

关于拓扑排序，还需要关注以下几点：

拓扑排序的结果可能不唯一，因为在构建过程中往往会出现多个入度为 0 的顶点，不同的选择顺序会产生不同的合法排序结果。

如果图中 存在环路，那么无法进行拓扑排序，因为无法找到入度为 0 的顶点作为起始顶点。

关键路径

关键路径是指 AOE 网（Activity On Edge Network）中，从源点到汇点所经过的 最长路径。这条路径决定了整个项目完成所需的最短时间，因此被称为 关键 路径。

AOE 网

AOE（Activity on Edge Network）网是一种以边表示活动或任务的网络模型。每条边代表一个任务或活动，而顶点通常表示事件，表示任务的开始或完成时间。

为了理解关键路径，首先需要明确 AOE 网中的以下概念：

• 源点：在 $AOE$ 网中仅有一个入度为 $0$ 的顶点，称为开始顶点，表示整个工程的开始。
• 汇点：在 $AOE$ 网中仅有一个出度为 $0$ 的顶点，称为结束结点，表示整个工程的结束。
• 关键路径的长度：完成整个工程的最短时间，也是 $AOE$ 网中从源点到汇点的最长路径。
• 关键活动：关键路径上的活动。
• 活动的时间余量：某个活动可以被延迟的最大时间，而不会影响整个项目的最短完成时间（总工期）。
• $ve(k)$：事件 $v_k$ 的最早可以发生时间。
• $vl(k)$：事件 $v_k$ 的最晚可以发生时间。

有几个概念比较重要，还需要进行进一步的阐述：

在 AOE 网中，边代表活动（Activity），顶点代表事件（Event）。

• 活动（边）：表示一个具体的工作、任务或操作，具有确定的持续时间。一个活动必须在其起点事件“发生”之后才能开始。
• 事件（顶点）：表示一个时间点，通常是某些活动的“开始”或“结束”条件已经满足，代表某种逻辑上的时刻状态。

通俗讲：活动是“做某事”，事件是“可以开始做某事的时间点”

在 AOE 网中，一个事件的“发生”是指其所有前驱活动都已完成，这标志着“条件成熟”，从该事件出发的活动才可能被启动。

两个关键时间：

事件发生的判断逻辑：

一个事件是否可以发生，不看它的出边活动，而是看它的所有前驱活动（入边）是否完成：

• 若某事件 i 的所有进入活动（任务）都已完成 → 则事件 i 发生；
• 一旦事件 i 发生，其所有出边活动 可以开始，但 不必须同时开始；
• 出边活动的实际开始时间取决于它们自身的调度灵活性（浮动时间）。

“活动的时间余量”在 AOE 网中指的是：

一个活动可以被延迟的最大时间，而不会影响整个项目的最短完成时间（总工期）。

首先，为什么要有时间余量呢？因为在 AOE 网络中，不是所有活动都在关键路径上。

• 关键路径上的活动：必须准时进行，没有时间余量（余量 = 0）
• 非关键路径上的活动：允许适当延迟，但必须不阻碍项目的最晚结束时间

时间余量可以通过以下数学公式计算：

对于一个活动 $A(i \rightarrow j)$，持续时间为 $d_{ij}$，其时间余量：

$$\text{时间余量} = vl(j) - ve(i) - d_{ij}$$

其中：

• $ve(i)$：起点事件 i 的最早发生时间
• $vl(j)$：终点事件 j 的最晚发生时间
• $d_{ij}$：活动持续时间

关键路径上的所有活动都是 关键活动，它是决定整个工程的关键因素，因此可通过加快关键活动来缩短整个工程的工期。