数组和特殊矩阵

⭐ 中优先级
真题练习
在选择题偶尔会考察，多维数组的存储是 和 矩阵的几种压缩存储方式 要了解一下。

多维数组的存储

在计算机内存中，数组元素是 连续存放 的。对于一个二维数组来说，它实际上只是对一维数组的一种逻辑抽象。理解其存储方式的关键在于：如何将二维坐标 $(i, j)$ 映射到一维的线性内存地址。

假设：

  • 数组的第一个元素起始地址为 $A$；
  • 每个元素占用 $B$ 个字节；
  • 数组一共有 $R$ 行、$C$ 列；

那么数组中元素 $a[i][j]$ 的存储地址为：

$$ \text{Addr}(a[i][j]) = A + (i \times C + j) \times B $$

其中：

  • $i \times C$ 表示从第 0 行到第 $i-1$ 行总共有多少个元素；
  • 再加上 $j$，就得到了在一维展开后对应的下标；
  • 乘以 $B$ 后，加上基址 $A$，就得到了该元素在内存中的实际地址。

举个 C 语言的示例进行说明，如果我们定义一个二维数组：

int a[2][3] = {{1, 2, 3}, {4, 5, 6}};

这个数组的内存布局可以视为一个一维数组，如下所示：

  +---------+---------+---------+---------+---------+---------+
  | a[0][0] | a[0][1] | a[0][2] | a[1][0] | a[1][1] | a[1][2] |
  +---------+---------+---------+---------+---------+---------+
0x100      0x104    0x108     0x10C     0x110     0x114

行主序和列主序

需要注意的是，不同语言对多维数组的存储顺序可能不同：

  • C / C++ 等主流编程语言：采用 行主序（Row-major order），即先存满一行，再存下一行。
  • Fortran / MATLAB：采用 列主序（Column-major order），即先存满一列，再存下一列。

如果按列主序存储，上面例子 a[2][3] 的内存布局会变为：

  +---------+---------+---------+---------+---------+---------+
  | a[0][0] | a[1][0] | a[0][1] | a[1][1] | a[0][2] | a[1][2] |
  +---------+---------+---------+---------+---------+---------+

特殊矩阵的压缩存储

对称矩阵

什么是 对称矩阵：对于矩阵$A$中的任意一个元素$a_{i, j}$都有 $a_{i, j} = a_{j ,i}$，

Produced by GNUPLOT 4.4 patchlevel 0

所以为了 节省存储空间，可以使用一位数组$B$进行存储

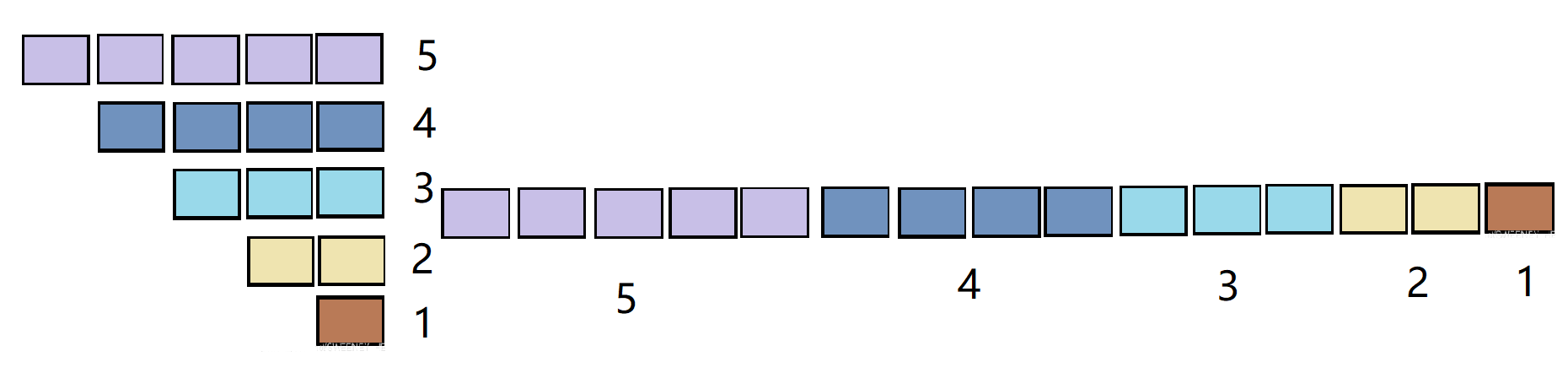
symmtry_matrix_storage

如何计算对称矩阵中元素的下标

$A$ 中的元素 $a_{i, j}$ 在数组 $B$ 的下标

$$k = 1 + 2 + \cdots + (i-1) + j - 1 = i(i-1)/2+j-1$$

元素为

$$a_{i, j} = \begin{cases} \frac{i(i-1)}{2}+j-1,\text{ } i \ge j \\ \frac{j(j-1)}{2}+i-1,\text{ } i \lt j \end{cases}$$

三角矩阵

{\displaystyle \mathbf {L} ={\begin{bmatrix}l_{1,1}&&\cdots &&0\\l_{2,1}&l_{2,2}&&(0)&\\l_{3,1}&l_{3,2}&\ddots &&\vdots \\\vdots &\vdots &\ddots &\ddots &\\l_{n,1}&l_{n,2}&\ldots &l_{n,n-1}&l_{n,n}\end{bmatrix}}}

下三角矩阵

{\displaystyle \mathbf {U} ={\begin{bmatrix}u_{1,1}&u_{1,2}&u_{1,3}&\ldots &u_{1,n}\\&u_{2,2}&u_{2,3}&\ldots &u_{2,n}\\\vdots &&\ddots &\ddots &\vdots \\&(0)&&\ddots &u_{n-1,n}\\0&&\cdots &&u_{n,n}\end{bmatrix}}}

上三角矩阵
  • 下三角矩阵 是一个方阵，其主对角线及其以下（右下部分）的所有元素都不为零，而主对角线以上的所有元素都为零。
  • 上三角矩阵  是一个方阵，其主对角线及其以上（左上部分）的所有元素都不为零，而主对角线以下的所有元素都为常数。
三角矩阵下标计算

以上三角矩阵 $A$ 为例，上半部分元素首先按序存储在一位数组 $B$ 中，在最后一个位置添加一个元素，用于存储下三角位置对应的元素

$A$ 中的元素 $a_{i, j}$ 在数组 $B$ 的下标

$$k = n + (n+1) _ \cdots + (n-i+2) + (j-i+1) - 1 = (i-1)(2n-i+2)/2 + (j-i)$$

元素为

$$a_{i, j} = \begin{cases} \frac{(i-1)(2n-i+2)}{2}+(j-i),\text{ } i \le j（\text{\small 上三角区和对角线元素}） \\ \frac{n(n+1)}{2},\text{ } i \gt j（\text{\small 下三角区元素}） \end{cases}$$

稀疏矩阵

稀疏矩阵（Sparse Matrix）是指在矩阵中大部分元素为零的矩阵。与之相对的是 稠密矩阵（Dense Matrix），即大部分元素非零。

$$ A_{6 \times 7} = \begin{bmatrix} 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 2 & 0 & 0 & 0 & 0 & 0 \\ 3 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 5 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 6 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 7 & 4 \end{bmatrix} $$

由于 稀疏矩阵 的非零元素远少于零元素，存储整个矩阵（包括所有零元素）会浪费大量空间。因此，稀疏矩阵通常使用特定的数据结构（三元组表 和 十字链表）来高效存储和操作，只保存非零元素及其位置信息。

三元组表

三元组表（Triple Table） 是一种稀疏矩阵的顺序存储方法。它利用三个一维数组（或一个结构体数组）分别存放非零元素的 行号、列号 和 数值，从而节省内存空间。

对于一个 $m \times n$ 的稀疏矩阵 $A$，若其中只有 $t$ 个非零元素，则三元组表的长度就是 $t$。存储时，一般约定按照 行序优先（先按行号从小到大排序，行号相同时再按列号从小到大）存放，便于后续矩阵运算和查找。

在程序实现时，常见的两种方式是：

  1. 分开存储法
    用三个等长的一维数组 row[]、col[] 和 val[] 分别保存行号、列号和数值。
  2. 结构体存储法
    定义一个结构体 Triple，包含 (row, col, value) 三个字段，再用一个一维数组 Triple data[t] 来存储。
#define MAXSIZE 100  // 最大非零元素个数

// 稀疏矩阵三元组表（分开存储）
typedef struct {
    int m, n, t;          // 矩阵的行数、列数、非零元素个数
    int row[MAXSIZE];     // 行号数组
    int col[MAXSIZE];     // 列号数组
    int val[MAXSIZE];     // 数值数组
} TSMatrix;
#define MAXSIZE 100  // 最大非零元素个数

// 三元组
typedef struct {
    int row, col;  // 行号、列号
    int val;       // 数值
} Triple;

// 稀疏矩阵三元组表（结构体存储）
typedef struct {
    int m, n, t;        // 矩阵的行数、列数、非零元素个数
    Triple data[MAXSIZE]; // 非零元素数组
} TSMatrix;

三元组表的优点是 存储结构简单、节省空间，但缺点是 随机访问代价较高 —— 若要访问某个元素，需要顺序扫描查找对应行列下标，适合用于矩阵转置、稀疏矩阵相加、输出等操作。

在实际应用中，如果需要频繁地进行按行、按列的运算，就会引入 十字链表 等更复杂的存储方式。

十字链表

十字链表（Cross List） 是一种用于稀疏矩阵的存储结构，它的核心思想是利用行方向和列方向两个链表同时组织非零元素，从而使得既能按行遍历，也能按列遍历，访问效率都较高。相比于普通的顺序存储或单一链表结构，十字链表在需要频繁进行矩阵运算、转置或按行按列混合访问的场景下具有明显优势。

下图给出了一个十字链表的实例：

3
1
1
3
2
2
-1
^
^
3
1
2
^
^
^
1
4
5
^
^
rhead
chead
0
0
5
0
-1
0
0
2
0
0
0

在十字链表中，每一个非零元素都会建立一个结点。该结点需要记录行号（i）、列号（j）、元素值（value），同时还要保存两个方向的指针：right 指针指向同一行中的下一个非零元素，down 指针指向同一列中的下一个非零元素。借助这两个指针，矩阵可以在行链和列链之间灵活切换，实现双向高效的访问。

为了快速定位某一行或某一列的首个非零元素，还需要额外设置行头指针数组（rhead）和列头指针数组（chead）。每一行和每一列都对应一个头指针，这些头指针并不存储具体数值，而是起到索引的作用，使得从某一行或某一列开始的遍历可以在常数时间内定位到第一个非零元素。

// 十字链表结点定义
typedef struct CrossListNode {
    int row;                    // 行号
    int col;                    // 列号
    int value;                  // 元素值
    struct CrossListNode* right;  // 指向同一行下一个非零元素
    struct CrossListNode* down;   // 指向同一列下一个非零元素
} CrossListNode;
// 十字链表结构
typedef struct {
    CrossListNode** rhead;      // 行头指针数组
    CrossListNode** chead;      // 列头指针数组
    int rows;                   // 矩阵行数
    int cols;                   // 矩阵列数
    int nums;                   // 非零元素个数
} CrossList;

十字链表的优势主要体现在三个方面：其一，空间效率高，仅存储非零元素及必要的指针；其二，支持按行或按列的双向遍历，在算法实现中非常灵活；其三，插入与删除操作方便，只需在相应行和列的链表中调整指针即可，而不必像顺序存储那样整体移动元素。因此，十字链表常被用于稀疏矩阵运算和图的邻接矩阵存储，是数据结构与图论中重要的一种存储方式。

三对角矩阵

三对角矩阵是一种特殊的稀疏矩阵，它除了主对角线外，只在其上下相邻的两条对角线上有非零元素，其余元素均为零。

$$\begin{vmatrix} a_{1,1} & a_{1,2} & & & & \\ a_{2,1} & a_{2,2} & a_{2,3} & & & \\ & a_{3,2} & a_{3,3} & a_{3,4} & & \\ & & \ddots & \ddots & \ddots & \\ & & & a_{n-1,n-2} & a_{n-1,n-1} & a_{n-1,n}\\ & & & & a_{n,n-1} & a_{n,n} \end{vmatrix}$$

由于仅有三条对角线是非零的，我们可以只存储这三条线来 节省空间（从 $n^2$ 降为 $3n-2$ 个数字）。

一种常用存储方式是使用三个长度为 n 的数组：

  • a[2...n]：下对角线（从第 2 行开始有值）
  • b[1...n]：主对角线
  • c[1...n-1]：上对角线（到第 n-1 行）